CodeIQ:点字ブロックで作る道順
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「点字ブロックで作る道順」(CodeIQ)を参照してください。
問題の概要
街を歩いていると、点字ブロック(視覚障害者誘導用ブロック)を多く目にします。
点字ブロックは「誘導ブロック(線状ブロック)」と「警告ブロック(点状ブロック)」の2種類があり、まっすぐ進む場所に誘導ブロックを配置、進路が曲がったり、行き止ったりする箇所に警告ブロックを配置します。
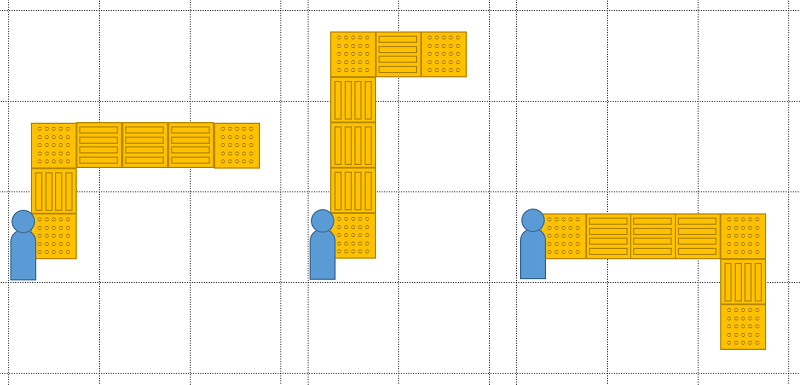
今回は以下のような格子状のマス目に対し、「マスの中央」と「マスの境界線をまたぐ方向」に2種類のブロックを配置し、あるスタート地点から順にマスを移動できるようにします。
なお、移動は必ず上下左右に配置するものとし、斜めに向けることはできません。
また、最初と最後は必ず警告ブロックになります。
標準入力から誘導ブロックと警告ブロックの数がスペース区切りで標準入力から与えられます。
このブロックをすべて配置するとき、一本の通路として配置できるパターンが何通りあるかを求め、標準出力に出力してください。
ループするような配置は考えないものとし、左右対称などの対称形も別々にカウントするものとします。
なお、ブロックは同じ位置に複数配置できません。
例えば、誘導ブロックが4個、警告ブロックが3個の場合、上の図のようなものを含めて16通りの配置が考えられますので、入出力は以下のようになります。
【入出力サンプル】
標準入力
4 3
標準出力
16
ブロックの数は合わせて25個まで対応できるようにしてください。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
class Route
attr_reader :tiled, :pos, :direction
# tiled 通った座標のハッシュ
# pos 座標
# direction 方向(上[0,1]、右[1,0]、下[0,-1]、左[-1,0])
# s まっすぐ進むブロックの残り数
# t 左右に曲がるブロックの誇り数
def initialize(tiled, pos, direction, s, t)
@tiled = tiled
@pos = pos
@direction = direction
@s = s
@t = t
end
def setGoal()
nxt_d = @direction
@pos = [@pos[0] + nxt_d[0], @pos[1] + nxt_d[1]]
if @tiled[@pos] then return false
else
@tiled[@pos] = true
return true
end
end
def nextAhead()
if (@s == 0) && (@t != 0) then return nil
else
nxt_p = [@pos[0] + @direction[0], @pos[1] + @direction[1]]
if @tiled[nxt_p] then return nil
else
nxt_d = @direction.dup
nxt_t = @tiled.dup
nxt_t[nxt_p] = true
return Route.new(nxt_t, nxt_p, nxt_d, @s-1, @t)
end
end
end
def nextRight()
if (@s != 0) && (@t == 0) then return nil
else
nd = {
[0,1] =>[1,0],
[1,0] =>[0,-1],
[0,-1]=>[-1,0],
[-1,0]=>[0,1]
}
nxt_p = [@pos[0] + @direction[0], @pos[1] + @direction[1]]
if @tiled[nxt_p] then return nil
else
nxt_d = nd[@direction]
nxt_t = @tiled.dup
nxt_t[nxt_p] = true
return Route.new(nxt_t, nxt_p, nxt_d, @s, @t-1)
end
end
end
def nextLeft()
if (@s != 0) && (@t == 0) then return nil
else
nd = {
[0,1] =>[-1,0],
[-1,0]=>[0,-1],
[0,-1]=>[1,0],
[1,0] =>[0,1]
}
nxt_p = [@pos[0] + @direction[0], @pos[1] + @direction[1]]
if @tiled[nxt_p] then return nil
else
nxt_d = nd[@direction]
nxt_t = @tiled.dup
nxt_t[nxt_p] = true
return Route.new(nxt_t, nxt_p, nxt_d, @s, @t-1)
end
end
end
end
def solve(m,n)
s = (m-(n-1))/2
t = n-2
if (s <= 0) || (t <= 0) then return 0 end
st = [0,0]
queue = [Route.new({st=>true}, st, [0,1], s, t)]
for _ in 0...(s+t)
nqueue = []
while !queue.empty?
route = queue.shift
a = route.nextAhead()
if a != nil then nqueue << a end
r = route.nextRight()
if r != nil then nqueue << r end
l = route.nextLeft()
if l != nil then nqueue << l end
end
queue = nqueue
end
cnt = 0
for q in queue
if q.setGoal() then
cnt += 1
end
end
return cnt
end
# main
while line = gets
line.strip!
if line.empty? then next end
m,n = line.split.map{|a| a.to_i}
p 4*solve(m,n)
end
解説
加えて問題の意味が読み取りにくいです。わかりにくいと思った部分を補足しておきます。
通路はマス目の中をたどるようにしなければなりません。点字ブロックはマス目の境界線の上にも配置されますが、境界線上を通るような通路はダメです。例の左端の図のスタート地点の次の「誘導ブロック(線状ブロック)」を除いて右に折れてからに追加すると下図のようになります。「--」がマスの境界線で、「誘導ブロック(線状ブロック)」が境界線上になってしまいます。
--■====■-- ■こういう配置はNGです。
考え方
前と左右に移動できる可能性があって、最大25のブロックがあ李ます。そして、ゴール地点からは進めませんがスタート地点は4方向に進めるので、最大で4*324くらいのパターンがあります。
これでは計算量が多すぎるので、いかにして計算量を減らすかというのがポイントになります。
まず、スタート地点からは1方向しか考えなくて良いというのは簡単にわかります。スタート地点からは上下左右に進めるとしても、上だけ考えて後は90度ずつ回転すれば同じです。
なので、スタートからは1方向だけ考えて、そのパターン数を4倍すれば良いことになります。
スタートとゴールは「警告ブロック(点状ブロック)」ですこれは考えなくても良いことがわかります。
スタートからの方向を1つに固定してしまえば単に初期値を与えるだけですし、ゴールからは進めないので関係ありません。
そして、よく考えると境界線上には「誘導ブロック(線状ブロック)」しかこないことがわかります。補足した通り、通路はマスの中を通らなければな李ません。もし、境界線上に「警告ブロック(点状ブロック)」が来ると境界線上に通路ができてしまいます。
境界線上には「誘導ブロック(線状ブロック)」しか配置されないなら、境界線上に配置される「誘導ブロック(線状ブロック)」を最初から除外してしまって、マスの中に配置されるブロックだけを考えれば十分ということになります。
これで計算量は相当減ります。
あと重要なのはブロックが交差した場合の判断です。
私はこれに関して良い方法を思いつきませんでした。なので単に連想配列を使ってチェックすることにしました。
main
入力値をパースして変数inputにとり、solve()に渡して結果を求めます。
solve()はスタートから1方向だけのパターン数を返すので4倍して印字します。
solve(m,n)
引数m,nは入力値を数値にしたものです。
sはマスの中に配置される「誘導ブロック(線状ブロック)」の数、tはスタートとゴール以外の「警告ブロック(点状ブロック)」の数です。
tは特に説明しなくてもわかるでしょう。
sは次のように考えます。線状ブロックと点状ブロックが交互に並んでいると仮定します。この場合、両端が点状ブロックなので点状ブロックが1つ多く、全体は奇数個です。点状ブロックを1つ除いて個数を1/2にすると線状ブロックの数になります(交互に並んでいる場合)。ここで点状ブロックの数をn(n>=2)、線状ブロックの数をmとするとコード中の式でマスの中に配置される線状ブロックの数になります。
92行目の条件文は通路を作れない入力値のエラーチェックです。
97〜114行目のループでマスの中に配置されるブロックを1個目(スタートの次)から順番に配置し、パターンを作ります。パターンはRouteクラスで管理します。94〜95行目で初期値を設定しています。初期値は座標[0,0]から上方向に進むと設定します。
97行目のforはブロックを1個ずつ配置するためのループで、100行目のwhileは前回のforループまでで列挙したパターン全てに対してブロックを1個追加するためのものです。
ブロックは線状ブロックと点状ブロックがありますが、点状ブロックは左右に曲がれるので右と左を区別してパターンを作ります(点状ブロックではなく、右矢印ブロックと左矢印ブロックがあるかのように考えます)。この処理をしているのが103〜110行目でroute.nextAhead()が線状ブロック、route.nextRight()が右矢印ブロック、route.nextLeft()が左矢印ブロックを追加したパターンを返します。いずれもブロックを使い切っていたり、通路が交差したりした場合はnilを返すので、nilが返ってきた場合は無視します。
117行目からの処理はゴールのブロックを置く処理です。のブロックが通路と交差することもあるのでここでチェックし、通路と交差しなかった場合だけを数えます。
ここでカウントした数が答えになります。
Routeクラス
ブロックの配置パターンを管理するクラスです。
メンバ変数は次の通りです。
tiled:ブロックを配置した座標を保持します。交差のチェックを高速にするためHashを使い{[x座標,y座標]=>true}という値を持ちます。
pos:最後の座標を保持します。RubyのHashは登録順が管理されている気もしますが、調べるのが面倒だったので変数を用意しました。
direction:次にブロックを置く方向(上外左右)を保持します。
s:線状ブロックの残り数です。
t:点状ブロックの残り数です。
Route#nextAhead(),nextRight(),nextLeft()
それぞれ、線状ブロック、右矢印ブロック(点状ブロックで次は右にブロックを置く)、左矢印ブロック(点状ブロックで次は左にブロックを置く)を配置する関数です。やっていることは大体同じなのでまとめて説明します。
最初の条件は配置しようとしているブロックが残っているかどうかのチェックです。ブロックが残っていなければそのパターンは作れないのでnilを返します。
ブロックが残っていれば配置します。@directionに前回のブロックに対してどの場所に今回のブロックを置くのかが指定されています。@directionは上[0,1]、右[1,0]、下[0,-1]、左[-1,0]のどれかが入っており、@posは前回ブロックを配置した座標なので、@posと@directionのx,y要素をそれぞれ足し合わせれば今回のブロックの座標(nxt_p)になります。
ブロックの座標(nxt_p)を求めたら、すでにブロックが配置されているかをチェックします。これは@tiled[nxt_p]がtrueならすでにブロックが置かれている座標なのでnilを返します。
そうでなければ、次にブロックを置く場所(nxt_d)、今回のブロックを配置した座標情報(nxt_t)、を作って新しいRouteインスタンスを生成して返します。nextRight()とnextLeft()は次にブロックを配置する場所が現在の方向に対して右と左になるので@directionから次の場所を求めます。定数ndがそのための連想配列でnextRight()は90度右、nextLeft()90度左に回転した方向を返します。
Route#setGoal()
ゴールのブロックをおいて交差をチェックします。
基本的にRoute#nextAhead()と同じですが、@s、@tにはゴールブロックが含まれていないのでチェックしません。
また、経路情報を更新する必要もないのでゴール位置にブロックがあるかないかだけをチェックし、ブロックがあればfalse、なければtrueを返します。
雑感
補足に書いたことを問題文から読み取るのに一番苦労しました。例の4と3のパターンを手で書いてみたら数が合わず、理由もわからないのでやめようかと思いました。NGの例として境界線上にブロックを並べるパターンを1つあげてくれれば良かったのにと思います。
解説の冒頭に難しかったと書きましたが、プログラム(アルゴリズム)以外の部分が難しかったんだな、と思います。境界線上には線状ブロックしか置かれず、考えなくて良いとか。でもまぁ、ある問題の見方を変えても同じという判断をするのもプログラミング能力の一部だからこれはこれで良いのですが、この問題に関してはマス目内だけにブロックを配置する問題があって、それをわかりにくくするために境界線上の要素をわざわざ追加したように思えるのがちょっとなぁ、という気分になります。