CodeIQ:投影図から想像する立体
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「投影図から想像する立体」(CodeIQ)を参照してください。
問題の概要
3次元の物体を図面に表すとき、投影図を使うことがあります。
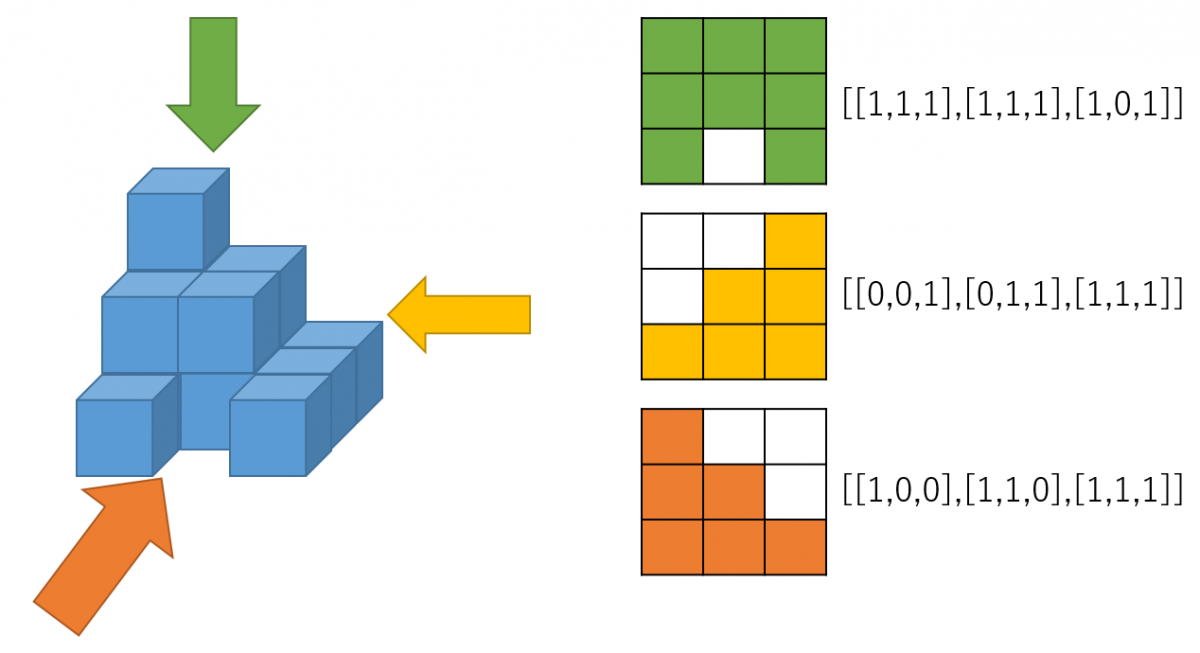
例えば、図の左側のようにブロックが積まれているとき、上面図・側面図・正面図を矢印の方向から見た図で考えると、図の右側のようになります。
このとき、ブロックが見える位置を「1」、見えない位置を「0」とし、上の段から順に右のように表現します。
この上面図、側面図、正面図の表現が標準入力から与えられるとき、考えられるブロックの配置が何通りあるかを求め、標準出力に出力してください。
なお、入力のサイズはいずれの面も3×3で固定とします。
また、ブロックの下には必ずブロックが必要で、空中に浮くブロックはないものとします。
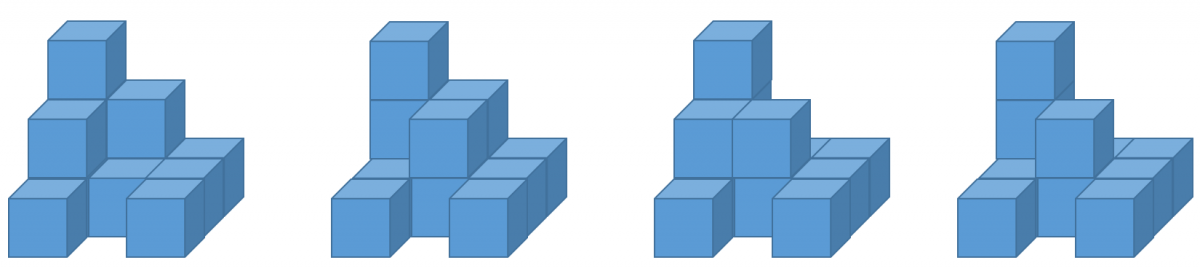
例えば、上記の場合は他に以下のパターンがあり、全部で5通りですので、以下のように出力します。
【入出力サンプル】
標準入力
[[1,1,1],[1,1,1],[1,0,1]]
[[0,0,1],[0,1,1],[1,1,1]]
[[1,0,0],[1,1,0],[1,1,1]]
標準出力
5
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 入力値をパースして数値の配列にする
def parseLine(line)
ret = []
line.scan(/\[(\d,\d,\d)\]/).each{|arr|
ret << arr[0].split(",").map{|c| c.to_i}
}
return ret
end
# 上から見た入力値から最大の図形を返す
def getBaseShapeTop(shape, top)
ret = [[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]]]
for h in 0...3
for d in 0...3
for w in 0...3
ret[h][d][w] = shape[h][d][w] & top[d][w]
end
end
end
return ret
end
# 右から見た入力値から最大の図形を返す
def getBaseShapeRight(shape, top)
ret = [[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]],]
for w in 0...3
for h in 0...3
ret[h][0][w] = shape[h][0][w] & top[h][2]
ret[h][1][w] = shape[h][1][w] & top[h][1]
ret[h][2][w] = shape[h][2][w] & top[h][0]
end
end
return ret
end
# 前から見た入力値から最大の図形を返す
def getBaseShapeFront(shape, front)
ret = [[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]],[[0,0,0],[0,0,0],[0,0,0]]]
for h in 0...3
for d in 0...3
for w in 0...3
ret[h][d][w] = shape[h][d][w] & front[h][w]
end
end
end
return ret
end
# 入力値から最大の図形を返す
def getBaseShape(top, right, front)
shape = [[[1,1,1],[1,1,1],[1,1,1]],[[1,1,1],[1,1,1],[1,1,1]],[[1,1,1],[1,1,1],[1,1,1]]]
shape = getBaseShapeTop(shape, top)
shape = getBaseShapeRight(shape, right)
shape = getBaseShapeFront(shape, front)
return shape
end
# 図形から上から見た場合の投影図を返す
def bitProjectionTop(s)
ret = 0
ret |= (s | (s >> 9) | (s >> 18)) & 0b000000001
ret |= (s | (s >> 9) | (s >> 18)) & 0b000000010
ret |= (s | (s >> 9) | (s >> 18)) & 0b000000100
ret |= (s | (s >> 9) | (s >> 18)) & 0b000001000
ret |= (s | (s >> 9) | (s >> 18)) & 0b000010000
ret |= (s | (s >> 9) | (s >> 18)) & 0b000100000
ret |= (s | (s >> 9) | (s >> 18)) & 0b001000000
ret |= (s | (s >> 9) | (s >> 18)) & 0b010000000
ret |= (s | (s >> 9) | (s >> 18)) & 0b100000000
return ret
end
# 図形から右から見た場合の投影図を返す
def bitProjectionRight(s)
ret = 0
ret |= ((s >> 6) | (s >> 7) | (s >> 8)) & 1
ret |= ( ((s >> 3) | (s >> 4) | (s >> 5)) & 1 ) << 1
ret |= ( (s | (s >> 1) | (s >> 2)) & 1 ) << 2
ret |= ( ((s >> 15) | (s >> 16) | (s >> 17)) & 1 ) << 3
ret |= ( ((s >> 12) | (s >> 13) | (s >> 14)) & 1 ) << 4
ret |= ( ((s >> 9) | (s >> 10) | (s >> 11)) & 1 ) << 5
ret |= ( ((s >> 24) | (s >> 25) | (s >> 26)) & 1 ) << 6
ret |= ( ((s >> 21) | (s >> 22) | (s >> 23)) & 1 ) << 7
ret |= ( ((s >> 18) | (s >> 19) | (s >> 20)) & 1 ) << 8
return ret
end
# 図形から前から見た場合の投影図を返す
def bitProjectionFront(s)
ret = 0
ret |= (s | (s >> 3) | (s >> 6)) & 0b000000001
ret |= (s | (s >> 3) | (s >> 6)) & 0b000000010
ret |= (s | (s >> 3) | (s >> 6)) & 0b000000100
ret |= ((s >> 6) | (s >> 9) | (s >> 12)) & 0b000001000
ret |= ((s >> 6) | (s >> 9) | (s >> 12)) & 0b000010000
ret |= ((s >> 6) | (s >> 9) | (s >> 12)) & 0b000100000
ret |= ((s >> 12) | (s >> 15) | (s >> 18)) & 0b001000000
ret |= ((s >> 12) | (s >> 15) | (s >> 18)) & 0b010000000
ret |= ((s >> 12) | (s >> 15) | (s >> 18)) & 0b100000000
return ret
end
# h,d,wのブロックを削除した投影図を返す。
# ブロックを取れない(ブロックがない、上にブロックがある)場合はnilを返す
# 3方向の入力値が一致しない場合もnilを返す
# 3方向の投影図が一致する場合はその図形を返す
# @param shape 図形のビット表現
# @param h,d,w 削除位置
# @param pj 入力された投影図のビット表現
def getNext(shape, h, d, w, pj)
i = 9*h+3*d+w
if (shape >> i) & 1 == 0 then return nil end
if (i >= 9) && ((shape >> (i-9)) & 1 == 1) then return nil end
mask = 0b111111111111111111111111111 ^ (1 << i)
nxt = shape & mask
if checkProjection(nxt, pj) then return nxt
else return nil
end
end
# 投影図が入力値と同じかをチェックする
def checkProjection(shape, pj)
# 投影図が同じかチェック
pt = bitProjectionTop(shape)
if pt != pj[0] then return false end
pr = bitProjectionRight(shape)
if pr != pj[1] then return false end
pf = bitProjectionFront(shape)
if pf != pj[2] then return false end
return true
end
def toBit(arr)
ret = 0
arr.each_with_index{|v, i|
ret |= (v<<i)
}
return ret
end
def shapeToBit(shape)
return toBit(shape.flatten)
end
def projectionToBit(proj)
return toBit(proj.flatten)
end
# 問題を解く
def solve(input)
projection = [projectionToBit(input[0]), projectionToBit(input[1]), projectionToBit(input[2])]
shape = getBaseShape(input[0], input[1], input[2])
b = shapeToBit(shape)
if checkProjection(b, projection) == false then return 0 end
queue = [b]
results = {b=>true}
while !queue.empty?
s = queue.shift
for h in 0...3
for d in 0...3
for w in 0...3
nxt = getNext(s, h, d, w, projection)
if nxt == nil then
next
else
if results[nxt] == nil
queue << nxt
results[nxt] = true
end
end
end
end
end
end
return results.size
end
# main
input = []
while line = gets
line.strip!
if line.empty? then next end
input << parseLine(line)
end
p solve(input)
解説
★★★の問題で相応に難しいです。この問題の難しさは3次元のデータの取り扱いによるプログラミング自体の難しさと計算量の2点があります。ただ、数学的な能力をそれほど要求されるわけではないので頑張ればできる問題と思います。
考え方
基本的な考え方はシンプルです。
入力値の投射図形から、その投射図形になる最大の(最もブロック数の多い)図形を求め、そこから任意のブロックを除いた時に入力値の投射図になる構成を選ぶというだけです。
- 3×3のブロックで埋め尽くされた立方体を用意する。
- 1の図形から上からの投射図でブロックがない場所のブロックを消す。
- 2の図形から右からの投射図でブロックがない場所のブロックを消す。
- 3の図形から前からの投射図でブロックがない場所のブロックを消す。
まず、3次元の図形を次のように表現します(例の一つ目の図の立体の場合)。
[
[[1,0,0],[0,0,0],[0,0,0]],
[[1,1,0],[1,1,0],[0,0,0]],
[[1,1,1],[1,1,1],[1,0,1]]
]
1行目が1番上の段で3行目が一番下の段、1つ目の配列が1番奥の行、3つ目の配列が手前の行です。つまり、左奥から右手前に向かってブロックのある場所を1、ない場所を0として表現します。投射図の方向から見て1段ずつ同じ場所の要素の値の論理和をとります。
私の立体図形の表現だと上から見た場合は、[[1,0,0],[0,0,0],[0,0,0]]と[[1,1,0],[1,1,0],[0,0,0]]と[[1,1,1],[1,1,1],[1,0,1]]の同じ場所の論理和をとるので[[1|1|1, 0|1|1, 0|0|1], [0|1|1, 0|1|1, 0|0|1], [0|0|1, 0|0|0, 0|0|1]] = [[1,1,1],[1,1,1].[1,0,1]]となり入力値と同じ値になります。
- キューに最大の図形を入れる。
- キューの先頭を取り出す。
- 左上奥から右下手前に向かってブロックがある場合、そのブロックを除く。
- ブロックを除いた図形の投射図を作る。
- 投射図が入力値と同じかをチェックし、違ったら無視する。同じ場合、以下の処理を行う。
- すでに出現した図形と同じなら無視する。
- 初めての図形ならキューに加え、結果をカウントアップする。
- キューが空になったらやめる
3次元図形、
[
[[1,0,0],[0,0,0],[0,0,0]],
[[1,1,0],[1,1,0],[0,0,0]],
[[1,1,1],[1,1,1],[1,0,1]]
]
の場合は0b1011111110000110110000000001と表現します。下位ビットが左上奥、上位ビットが右下手前と配列表現とは逆にした方が扱いが簡単です。
main
入力値をパースして変数inputにとり、solve()に渡して結果を求めます。
parseLine(line)
入力値1行分を数値の配列にします。
正規表現で0/1を取り出して数値に変換し、2次元配列を返します。
solve(input)
引数inputは入力値を数値の配列にしたものです。
戻り値は答えのパターン数です。
158行目では投射図を[上、右、前]それぞれの配列をビット表現に直したものを作っています。
159行目で投射図から求められる最大の3次元図形(配列表現)を作成し、159行目でビット表現に変換します。
162行目の処理は入力値から求められる最大の図形がそもそも妥当かをチェックしています。妥当な図形にならない場合は結果0なのでこの時点で0を返して処理をやめます。
入力値が妥当ならqueueに初期値として追加します(164行目)。
165行目のresultsは同じ図形が現れたかのチェックと結果をカウントするための領域です。Hashを使用しているのはArray.include?よりずっと早くチェックできるからです(ちなみに、resultsをArrayにしてArray.include?でチェックするとテストケースの最悪のパターンでは時間切れになります)。
あとはキューに図形がある限り(167〜185行目)、キューの先頭を取り出し(168行目)、左上奥から右下手前に向かってブロックを選び(170〜184行目のh,d,w)、選んだ場所のブロックを削除し(173行目)、それが投射図と一致しなければ無視し(175〜176行目)、一致するならqueueとresultsに追加する(177〜181行目)という処理をして結果を求めます。
resultsには投射図が入力値と同じになる3次元図形のデータが重複なく入っているので、その数が答えになります(187行目)。
projectionToBit(proj)、shapeToBit(shape)、toBit(arr)
配列をビット表現に変換します。
projectionToBit()は投射図、shapeToBit()3次元図形用ですがtoBit()のラッパーにすぎません。
toBit()は平滑化(多次元配列を1次元配列にしたもの)を受け取り、ビット表現にします。考え方に書いた通り最下位ビットが配列の0番目の要素、最上位ビットが配列の最後の要素になります。
checkProjection(shape, pj)
3次元図形と投射図のビット表現を引数に取り、上右前それぞれの方向の投射図が一致するかをチェックします。全て一致する場合はtrue、そうでなければfalseを返します。
3次元図形を投射図にするのはbitProjectionTop()、bitProjectionRight()、bitProjectionFront()で行います。
bitProjectionTop(shape)、bitProjectionRight(shape)、bitProjectionFront(shape)
それぞれ3次元図形を上、右、前から見た場合の投射図を求めます。
いずれも引数shapeは3次元図形のビット表現です。
これらの処理は考え方に書いた通りで、見ている方向から重なる位置のビットの論理和をとって加算します。
(s | (s >> 9) | (s >> 18))の様になっている部分が重なり部分の足し合わせで、0b000000001〜0b100000000までの値でマスクしているのは計算している場所以外を無視するためです。
上と前は計算が簡単ですが、右からは面倒くさいです。
右からの投射図は左上手前が最下位ビット、右下奥が最上位ビットになるのでそれを考慮して計算します。上と前からは必要なだけしかビットシフトしていませんが、右からの場合は計算対象のビットを一旦最下位ビットにずらして1でマスクした後、必要なだけ左シフトで結果の位置に戻しています。
getBaseShape(top, right, front)
投影図から3次元の最大図形を求めます。
この関数は入力値、戻り値とも配列表現です。
内部処理は3×3の領域が全部1の3次元配列に順次getBaseShapeTop()、getBaseShapeRight()、getBaseShapeFront()を適用しているだけです。
getBaseShapeTop(shape, top)、getBaseShapeRight(shape, right)、getBaseShape Front(shape, front)
引数shapeの3次元図形(配列表現)からtop、right、frontの投影図に必要ないブロックを削除します。
基本的に同じ処理なのでgetBaseShapeTop()だけを説明すると、1〜3番の段を順次取り出し、投影図と同じ場所の論理積をとります。投影図はブロックがない場所が0なので、これでその段でブロックがない場所を覗くことができます。
右からの投影図は左上手前が最初、右下奥が最後(上と前は左上奥が最初、右下手前が最後)で向きが違うのでその部分がけ異なる処理になっています(30〜32行目)。
雑感
結構しんどい問題でした。図形の問題も2次元ならそれほどでもありませんが、3次元になると数倍難しくなります。
ちなみに、私は問題の通り右方向から扱いましたが、右方向の値は反転して左方向から扱う様にした方がコードが単純になったと思います(左上奥が最初で右下手前が最後に統一できるので)。