CodeIQ：「レッド・アンド・ホワイト」問題

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「「レッド・アンド・ホワイト」問題」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

マス目が横に直線状に並んでいます。
マス目は左右にどこまでも続いているものとします。
マス目はすべて白色で塗られています。
このうちの 1 つを赤色で塗ります。
以降、次のルールに従って、マス目の色を塗り替えていきます。
1 秒後、左右隣のマス目の色が白赤または赤白となるマス目を全て赤色で塗り、そうでないマス目（つまり左右隣が白白または赤赤）を全て白色で塗ります。
以降、同様に、1 秒ごとに赤白でマス目を塗り替えていきます。
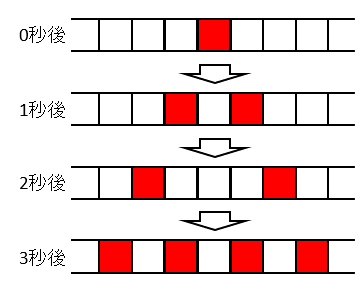
以下は、初期状態（0 秒後）から始めて、1 秒後、2 秒後、3 秒後の様子を示しています。

自然数 n に対し、n 秒後の赤色のマス目の個数を F(n) と定義します。
例えば F(1) = 2，F(2) = 2，F(3) = 4，F(4) = 2 です。
同様に、F(10) = 4，F(31) = 32，F(1023) = 1024，F(12345) = 64 となることが確かめられます。

標準入力から、自然数 n（1 ≦ n ≦ 10⁸）が与えられます。
標準出力に F(n) の値を出力するプログラムを書いてください。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

# OEIS A001316
# a(n) = 2 ^ (number of 1's in binary form of (n-1)).
# プログラムではnは0始まりなので1を引かない
def solve(n)
	bits = n.to_s(2).count('1')
	return 2**bits
end

#main
while line = gets
	line.strip!
	if line.empty? then next end

	n = line.to_i
end

p solve(n)

解説

この問題は自力で解くならば、かなり数学的な能力を要求される問題です。
ただし、コンピュータの世界では有名な「セルオートマトン」なので調べてなんとかすることができます。

1次元セルオートマトン

この問題を読んで最初に「あぁ、1次元セルオートマトンだ」と思いました。そして多分「シェルピンスキーのギャスケット」じゃないかなと直感し、シミュレーションを書いて確認しました。大当たりです。

OEIS

これほど有名なものならその数列がOEISにないはずはありません。
数列を生成する式も沢山あります（MathematicaやMapleで書かれているのでよくわからないのがほとんどですが）。ただし、問題は計算量です。1段ずつ動的計画法などで計算するのは時間的に大丈夫か確信が持てないので、与えられたn段目の数を直接求められる式を探した結果見つけたのがコードの式です。

ビットを数える

コードの式はn（0始まり）のバイナリ値のうち1の数で2を乗じたものです。
この方法で一番ネックになるのがビットを数える方法です。C/C++だと有名なビット演算を使った方法があるのですが、Rubyだと関数か何かが用意されてないかと思って調べました。
そうしたら文字列にして1の数を数えるのが最速ということです。実際やってみたら一瞬で終わります。これには驚きました。

雑感

「最短距離で往復できる形は？」と1日違いで公開された問題で、両方とも数学的能力が問われる問題です。「最短距離で往復できる形は？」はかなりプログラミングの問題としてどうかと思う部分がありますが、こちらはそうでもありません。
多分、こちらの問題はプログラマにとっては割と一般的な知識を元に調べることができる問題だからだと思います。

それとは別に、このセルオートマトンのパターンが正の整数のビットの1の数と関係があるというのは面白いと思いました。