CodeIQ：最短距離で往復できる形は？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「最短距離で往復できる形は？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

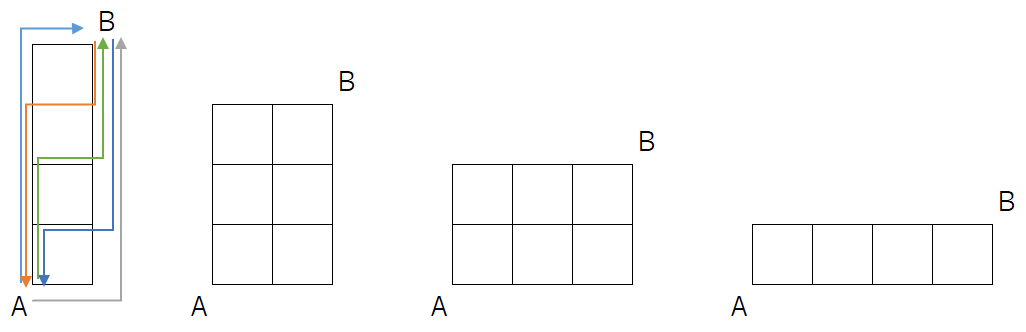
格子状の道路があり、左下のA点から右上のB点まで格子状の道路を最短距離で移動し、またB点からA点に最短距離で戻ってくることを繰り返します。
このとき、一度通ったルートとは異なる経路を通るものとします。
すべてのパターンを通ったとき、最終的にA点で終わるような道を考えます。
例えば、AからBまでの移動距離が5なのは以下の4通りがありますが、そのうち、最終的にA点で終わるのは中央の2通りです。
（両端の場合は、左端の道順のようにB点で終わる）

AからBまでの移動距離 n が標準入力から与えられたとき、最終的にA点で終わる形のうち、横幅が最小になるものを求め、その横幅を標準出力に出力してください。
A点で終わるものがない場合、0を出力してください。
(なお、n は最大で99999とします。)

上記のように n = 5 のときは横幅が2のときが最小ですので、標準出力に2を出力します。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

# 因数２の個数を比較する問題（2015年東大理科5）［D］
# （参考）http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14148239439
def solve(n)
	# nが偶数の場合必ず結果は1になる。
	# 縦：n-1、横：1の場合、ルートの数はn!/(1!*(n-1)!) = nであり偶数となる。
	# 問題からスタート地点に戻ってこれる条件はルートのパターン数が偶数の時なので、この場合は必ず横1になる
	if n % 2 == 0 then return 1 end

	mx = (Math.log2(n)).ceil
	for i in 1...mx
		d = 2**i
		nd = d * 2

		k = n % d
#		puts "d=" + d.to_s + ", nd=" + nd.to_s + ", k=" + k.to_s + ", n-k=" + (n-k).to_s + ",k+1=" + (k+1).to_s

		if (n-k) % nd == 0 && (k+1) % d == 0 && (k+1) % nd != 0 then return k+1 end
	end
	return 0
end


while line = gets
	line.strip!
	if line.empty? then next end

	n = line.to_i
end

p solve(n)

解説

この問題はコードの参考に書いてある通り、東大の入試問題と同じです。
プログラムは簡単ですが、数学的に私にはよくわかっていないのでほとんど解説できません。

考えた事

経路のパターンは調べると簡単にわかります。
縦横の辺の数をx,yとすると(x+y)!/(x!*y!)がパターン数になります。今回の問題ではn=x+yで横の辺の数iを変化させるとするとn!/((n-i)!*i!)でi<=n/2（端数切り上げ）までで最小となるものというのが答えの単純な考え方でしょう。

しかし、前述の式を元にいろいろやりましたが、最大値の99999に近い数では全然時間が足りません。単純にn!/((n-i)!*i!)ではダメ、少し計算量を減らすため_nC_i/(n-i)!にしてもダメです。bigintegerにしてもとんでもない数値になるため掛け算だけで非常に時間がかかってしまいます。
ならば、因数分解を組み合わせたら、これもダメ。さらに毎回全ての数をかけるのをやめて動的計画法で増減した分だけ計算してもダメ。

2ちゃんねるに何か書いてないかと思ってみたら、東大の入試問題と同じ問題と。
それで東大の数学の過去問を探し、2015年の問題に見つけたので解法を検索して見つけたのがプログラムの解き方です。
考え方は参考URLを参照してください。

雑感

さすがにこの問題はプログラミングの問題としてはどうでしょう？
解凍のコードのような数学的に解いた結果をプログラムするしかないというのは私としてはプログラム能力を測る問題としてはどうかと思います。