神尾ソフトウェア研究所
K=!0
CodeIQ:【コーエーテクモからの挑戦状!】敵本陣を攻め落とせ!
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「【コーエーテクモからの挑戦状!】敵本陣を攻め落とせ!」(CodeIQ)を参照してください。
問題の概要
問題を引用します。
敵本陣まであと一歩というところまで来ました。
勝利は目前ですが、敵の援軍が向かっているという情報が入りました。
【問題】
7×7マスのグリッド状のマップが与えられます。
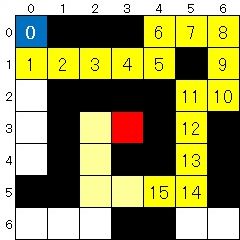
次の図のように、自陣は(0, 0)の地点(青い部分)、敵陣は(3, 3)の地点(赤い部分)にいます。
黒いマスは移動することができません。また、1マス移動するのに1日かかります。
このとき、自陣から敵陣まで15日以内に到達できるかどうかを判定するプログラムを書いてください。
【例】
この場合は8日で到達することができます。
この場合は、最短経路でも15日以内に到達することができません。
【入力】
標準入力から7行の文字列が与えられます。
各行の文字は「*」「o」「x」のいずれかで、7文字あります。
「*」は自陣または敵陣を表し、1行目の1文字目と4行目の4文字目にのみ現れます。
「o」は通過できる箇所、「x」は通過できない箇所を表します。
<出力>
自陣から敵陣まで15日以内に到達できる場合は「yes」、到達できない場合は「no」と出力してください。
【入出力サンプル】
Input
*oxxooo
oooooxo
oxxxxoo
oxo*xox
oooxxox
xxoooox
oooxxoo
Output
yes
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
$Map = []
def solve()
memo = Array.new(7){ Array.new(7, 65535) }
memo[0][0] = 0
queue = [[0,0]]
dir = [[-1,0], [0,1], [1,0], [0,-1]]
while !queue.empty?
now = queue.shift
return memo[now[0]][now[1]] if (now != [0,0]) && ($Map[now[0]][now[1]] == '*')
for d in dir
nxt = [now[0]+d[0], now[1]+d[1]]
next if (nxt[0] < 0) || (nxt[1] < 0) || (nxt[0] >=7) || (nxt[1] >=7)
next if $Map[nxt[0]][nxt[1]] == 'x'
next if memo[nxt[0]][nxt[1]] < 65535
memo[nxt[0]][nxt[1]] = memo[now[0]][now[1]] + 1
queue << nxt
end
end
return 65536
end
# main
while line = gets
line.strip!
next if line.empty?
$Map << line
end
ret = solve()
if ret <= 15 then puts 'yes'
else puts 'no'
end
解説
基本的な最短経路探索の問題です。
考え方
スタート地点からゴールまでの最短経路を求め、その移動距離が15以下かどうかを判定するだけです。
最短経路探索は問題に何度も出てきているので説明しません。
main
入力値kを二次元配列にして$Mapに保持し、solve()を呼びます。
戻り値が15以下かどうかを判定し、15以下ならyes、そうで無ければnoを印字します。
solve()
普通の幅優先探索を用いた最短経路探索です。
memoに各マスにたどり着くために必要な移動回数が保持されるので、ゴール地点の値を返せば良いわけです。
最短経路探索のプログラムは何度も記事にしているので省略します。
雑感
幅優先探索を使った最短経路探索の問題としては基本的で良いと思います。