CodeIQ:集合写真できれいに写る配置は何通り?
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「集合写真できれいに写る配置は何通り?」(CodeIQ)を参照してください。
問題の概要
みんなで集合写真を撮るときの並び方の配置を考えます。
人数が少なければ一列に並ぶこともありますが、横に長くなると図のように複数列に並ぶことがあります。
複数列に並ぶときは、互い違いに並ばないと全員の顔が見えないので、前の人の間から顔が見えるように並びます。
また、隣の人とは間を空けずに並ぶものとし、後ろに行けば行くほど人数が少なくなるものとします。
標準入力から人数 n が与えられたとき、n人が並ぶときの並び方が何通りあるかを求め、標準出力に出力してください。
(個人は区別せず、その配置だけを考えます。)
なお、n は 1≦n≦200を満たす整数とします。
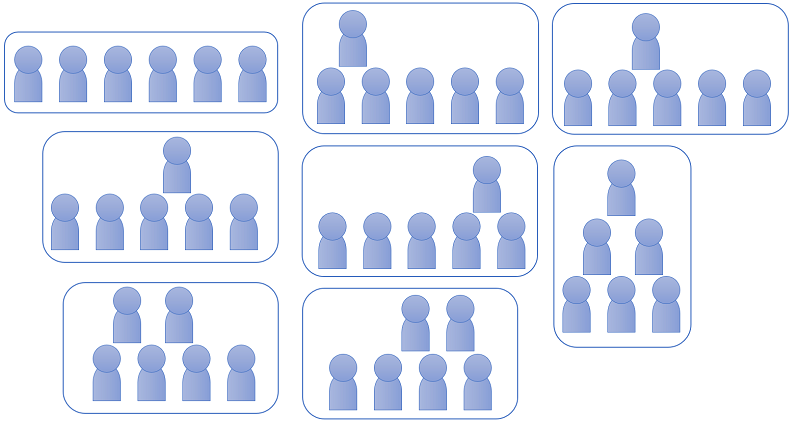
例えば、n=6 のとき、以下の8通りがあります。
【入出力サンプル】
標準入力
6
標準出力
8
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
$Memo = {}
def solve(n, b)
return $Memo[[n,b]] if $Memo[[n,b]] != nil
return 1 if n == 0
return 0 if( n <= b)
ret = 0
for i in (b+1)..n
r = solve(n-i, i)
if b == 0 then ret += r
else ret += (i-b) * r
end
end
$Memo[[n,b]] = ret
return ret
end
# main
while line = gets
line.strip!
next if line.empty?
p solve(line.to_i, 0)
end
解説
考え方
そうすると、i列目にn人並べた時、i+1列目にはn+1人以上を配置することになります。
当然、残りの人数がi列目に並べた人数以下になったらダメです。
i列目とi+1列目に配置可能な場合、(i+1列目の人数 - i列目の人数)パターンの並べ方があります。
更にi+1列目以上の並び方がm通りある場合、i列目以上の全ての並び方は(i+1列目の人数 - i列目の人数)× mです。
なので再帰でシンプルに求めることができます。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n, b)
nは残りの人数、bは一つ前の列の人数です。
$Memoに値がある場合、そのパターンは計算済みなのでその値を返します。
nが0の場合、並べ終わっているので1を返します。
n ≦ bの場合、問題の条件を満たせないので0を返します。
retはパターン数の合計です。
b以上n以下の範囲でその列に並べる人数を決めます。
solve(n-i, i)と再帰呼び出しし、上の列のパターン数を求めます。
bが0の場合、つまり一番下の列の場合は前の列の間に配置することができないので、間のパターンは常に1です。なので再帰呼び出ししたsolve()の結果をretにそのまま加えます。
b > 0の場合、考え方に書いた通り、前の列の人数との差だけ配置パターンがあるので(i-b)×再帰呼び出ししたsolve()の結果をretに加えます。
最終的に戻ってきたときのretが答えです。
雑感
本出題者の最後の問題でした。
私がCodeIQの問題をやり始めてからほぼ毎週出題されていました。これは大変なことです。
非常に勉強になりましたし、感謝しております。
ありがとうございました。