CodeIQ：同じ数を表示し続ける7セグメントディスプレイ

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「同じ数を表示し続ける7セグメントディスプレイ」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

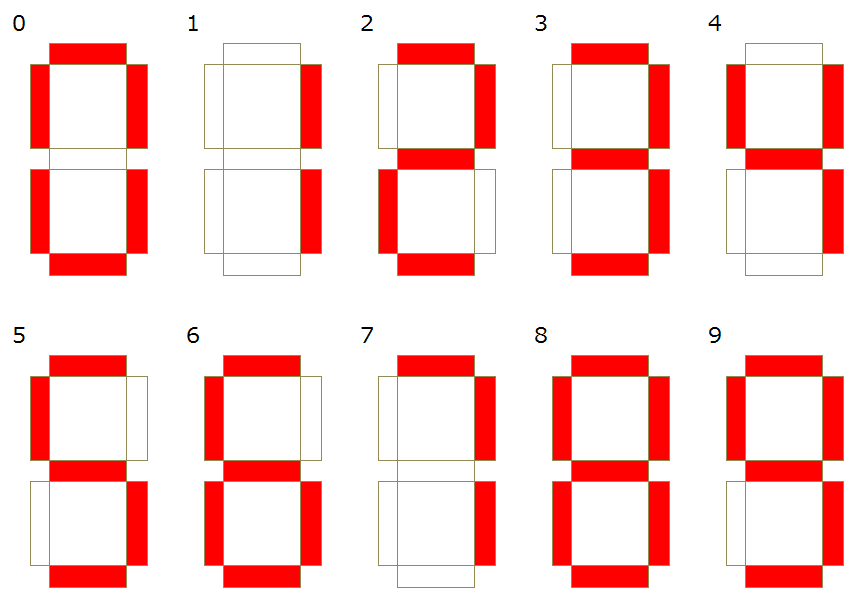
7セグメントディスプレイは7箇所の点灯の有無で数字を表示します。

この7セグメントディスプレイを横に並べて数を表示したとき、点灯している場所を数え、各桁での個数の「積」を次に表示します。

例えば、「718」からスタートすると、「7」は3箇所、「1」は2箇所、「8」は7箇所が点灯しているので、3×2×7=42を計算し、次に「42」を表示します。
また、「42」において、「4」は4箇所、「2」は5箇所が点灯しているので、4×5=20より次に「20」を表示します。
次に「20」において、「2」は5箇所、「0」は6箇所が点灯しているので、5×6=30より次に「30」を表示します。
さらに「30」において、「3」は5箇所、「0」は6箇所が点灯しているので、5×6=30より次に「30」を表示します。

つまり、「718」から始まると「718」→「42」→「20」→「30」→「30」→…というように「30」が続くようになります。
このとき、登場する数は「718」「42」「20」「30」の4種類だけです。

標準入力から整数 n が与えられたとき、上記の処理を行って過去に表示した数が再度表示されるまで探索したとき、登場する数がいくつあるか求め、その数を標準出力に出力してください。
なお、n は符号なし32ビット整数型の範囲(0～4,294,967,295)とします。

【入出力サンプル】
標準入力

718

標準出力

4

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

PTN = [6, 2, 5, 5, 4, 5, 6, 3, 7, 6]

def count(n)
	ret = 1
	loop{
		m = n % 10
		n /= 10
		ret *= PTN[m]
		break if n == 0
	}
	return ret
end

def solve(n)
	lst = {n => true}
	cnt = 0

	loop{
		cnt += 1
		n = count(n)
		if lst[n] then break
		else lst[n] = true
		end
	}

	return cnt
end

# main
while line = gets
	line.strip!
	next if line.empty?

	p solve(line.to_i)
end

解説

この出題者の問題としてはすごく簡単です。

考え方

問題の通りに実装すれば良いです。

0〜9の各数を7セグメントディスプレイで表示した時、点灯した場所の数はリストにしておけば十分です。
後は一桁ずつ問題の通りに計算し、同じものが現れるまで繰り返せば良いです。
収束は速いので計算量は問題ありません。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(n)

lstは{過去に現れた数 => true}という連想配列で、同じ数が現れたかのチェックに使います。
cntは繰り返しになるまでの回数で答えです。

lstに同じ数が現れるまでcount()を呼び出します。
同じ数が現れた時のcntを返します。

count(n)

PTNには0〜9の各数の7セグメントディスプレイの点灯位置の数のリストです。
1桁ずつ数を求め、PTNから7セグメントディスプレイの点灯位置の数を求めて掛け合わせます。

雑感

最初にも書きましたがこの出題者の問題としてはものすごく簡単です。
何か引っ掛けがあるのかと疑うレベルでしたが、そんなものもありませんでした。