CodeIQ：カエル跳びゲームを一般化して！

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「カエル跳びゲームを一般化して！」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

パズルで有名な「カエル跳びゲーム」を一般化したものを考えます。
n 個のマスがあり、左側から a マスには右に進むa匹のカエルが、右側から b マスには左に進むb匹のカエルがいます。
1つのマスには1匹のカエルしか入れられず、一度に1匹のカエルを移動します。

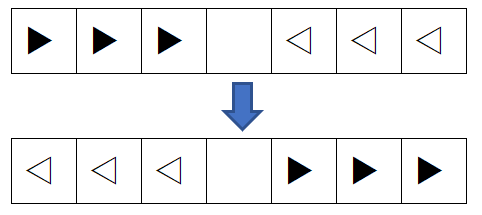
このカエルの位置を左右入れ替えることを考えます。
（右向きのカエルをすべて右側に、左向きのカエルをすべて左端に寄せるまで繰り返します。）

それぞれのカエルは、進む方向の隣のマスが空いていれば、その場所に移動できます。
また、隣に相手のカエルがいても、その先が空いていれば、一マスだけ飛び越えることができます。
二匹以上のカエルは飛び越えることはできませんし、同じ向きのカエルを飛び越えることもできません。
当然、逆方向に進むこともできません。

この操作を行い、最短の回数で移動するときの移動回数を求めてください。
なお、それぞれの向きのカエルを交互に移動する必要はありませんので、どちらから始めても構いませんし、同じ向きのカエルを連続して動かしても構いません。

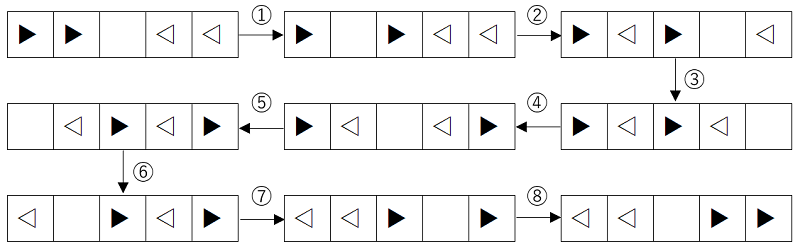
例えば、n = 5, a = 2, b = 2 のとき、以下の図のような手順で移動すると、8回で移動できます。

標準入力から n, a, b がスペースで区切って与えられますので、最短の移動回数を標準出力に出力してください。
なお、n, a, b は n > a + b を満たす整数で、n は最大で14とします。

【入出力サンプル】
標準入力

5 2 2

標準出力

8

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby
$Min = 0xFFFFFFFF
$Memo = {}

def move(ed, arr, m, cnt)
	# すでに同じパターンがあったか
	if $Memo[arr] != nil then return
	else $Memo[arr] = 0xFFFFFFFF
	end

	# 終了チェック
	if arr == ed then
		$Min = cnt
		$Memo[arr] = cnt
		return
	end

	# 現在のパターンより少ないパターンがすでに見つかっている
	if cnt >= $Min then
		$Memo[arr] = cnt+1
		return
	end

	for i in 0...m
		if arr[i] == 'a' then
			next if i+1 >= m	# 右端
			if arr[i+1] == 'a' then next	# 進行方向がa
			elsif arr[i+1] == 'b'	# 隣がb
				if i+2 >= m then next	# 右端
				elsif arr[i+2] != ' ' then next	# 空き場所ではない
				else j = i+2
				end
			else j = i+1	# 隣が空白
			end
		elsif arr[i] == 'b' then
			next if i-1 < 0		# 左端
			if arr[i-1] == 'b' then next	# 進行方向がb
			elsif arr[i-1] == 'a' then	# 隣がa
				if i-2 < 0 then next	# 左端
				elsif arr[i-2] != ' ' then next	# 空き場所ではない
				else j = i-2
				end
			else j = i-1
			end
		else next
		end

		# 次のパターン
		nxt = arr.dup
#		printf("nxt=%s, i=%d, j=%d\n", nxt, i, j)
		nxt[j] = nxt[i]
		nxt[i] = ' '


		# 継続
		move(ed, nxt, m, cnt+1)
	end
end

def solve(m, a, b)
	st = 'a' * a + ' ' * (m-a-b) + 'b' * b
	ed = 'b' * b + ' ' * (m-a-b) + 'a' * a

	move(ed, st, m, 0)
end

# main
while line = gets
	line.strip!
	next if line.empty?

	m, a, b = line.split.map{|v| v.to_i}
	solve(m, a, b)
	p $Min
end

解説

★★の問題ですが難しいと思います。
私のコードはテストケースはパスしていますが、パターンによっては1秒以内に終わるかどうか微妙な場合があります。

考え方

基本的に単純なメモ化再起です。

カエルの移動は再起で簡単に表せるのは容易にわかります。
カエルの並びを"aaa bbb"のような文字列で表し、ルール通りに再起で移動します。

最小手数を求めるので、答えにたどり着くごとに最小手数を更新します。
あるパターンの探索手数がその時の最小値以上になったらそれ以上の計算はうち切れるので打ち切ります。
また、メモですが答えに到達した時はカエルの並びに対してその手数を値としてメモしますが、打ち切った時はその時点の最小手数より大きい値をメモしておきます。これで同一パターンの再計算を省きます。

このようにして残った最小手数が答えになります。

main

入力値を数値にしてsolve()に渡し、結果を印字します。
$Minは最小手数、$Memoはメモを保持します。

solve(n)

stは開始時の配置、edは終了時の配置です。
move()にst、ed、m（入力値）、操作回数を渡して答えを求めます。

move(ed, arr, m, cnt)

カエルの移動を再起で処理し、最小手数を求めます。
edは終了チェックのための配置パターン文字列です。
arrは現在の配置の文字列です。
mは入力値です。
cntは現在の手数です。

まず、$Memoに結果があればそれを返します。なければ0xFFFFFFFF（非常に大きな値）にしておきます。これは再度そのパターンが現れた時無視するためです。

arrがedと同じなら移動終了です。
この時のcntを$Minにして、同時に$Memoを更新します。

cntが$Min以上になっている場合、それ以上の計算は無駄なのでやめます。

24〜46行目の処理はルール通りの移動です。

nxtにカエルを移動した後のパターンを作成し、move()を再帰呼び出しします。

move()が最終的に戻ってきたら$Minに答えが残ります。

雑感

この文章を書いているのが問題を解いてから大分経っているのでうろ覚えになっていますが、確か入力パターンによっては1秒で終わるかどうか微妙な感じだったと思います。多分、もっと良い方法があるのだと思います。
ちなみに、最初にやった時、aとbは同じ数でないことはわかっていたのですが、スペースが1個だけと思い込んでいて間違えました。