CodeIQ:目盛りの消えた円
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「目盛りの消えた円」(CodeIQ)を参照してください。
問題の概要
有名なパズル問題の一つに「Spacer Ruler(Wikipedia)」があります。
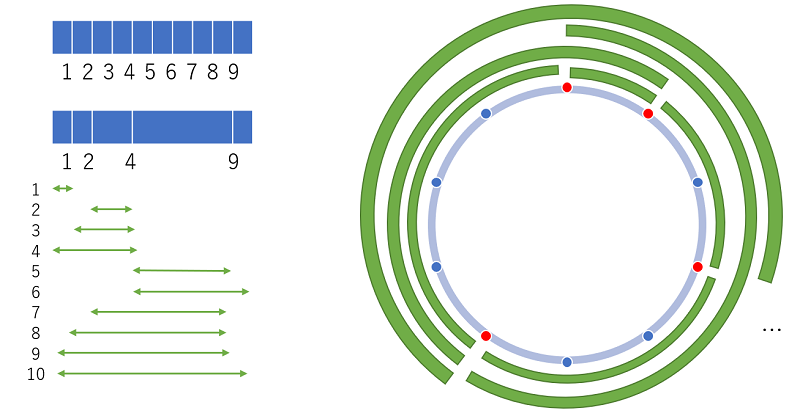
「目盛りの消えたものさし」とも言われ、できるだけ少ない目盛りの数で1cm単位の整数を測ります。
例えば、1cm刻みで目盛りが付いている長さ10cmのものさしの場合、左図の下側にある4つの目盛りが残っていると、それを組み合わせて図のように1cm~10cmまで測ることが可能です。
これを右図のように円形で考えてみます。
円周を n 個に分割した目盛りのうち、できるだけ多くの目盛りを消して1~nまでを測ります。
例えば、n = 10 のとき、右図の赤色の4点だけ残すと1~nまでを測れます。
3点だけ残して、1~10までを測ることはできませんので、少なくとも4点が必要です。
標準入力から n が与えられたとき、残った目盛りの数が最も少なくなる場合を求め、その残った個数を標準出力に出力してください。
なお、n は30以下の整数とします。
【入出力サンプル】
標準入力
10
標準出力
4
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
$Memo = []
def addVals(n, bef, i)
ret = []
bef.each{|j|
ret << i - j
ret << n + j - i
}
return ret
end
def add(n, bef, vals)
ret = {}
for i in (bef.last+1)...n
nxt = bef + [i]
nvals = vals + addVals(n, bef, i)
nvals = nvals.uniq.sort
ret[nxt] = nvals
end
return ret
end
def merge(to, from, memo)
from.each{|pts, vals|
next if memo[vals] != nil
next if to[pts] != nil
to[pts] = vals
memo[vals] = true
}
return to
end
def solve(n)
checker = (1..n).to_a
for i in 1...n
lasts = $Memo[i-1]
nxts = {}
memo = {}
lasts.each{|bef, vals|
news = add(n, bef, vals)
news.each{|pts, nvals|
if nvals == checker then
# printf("pts=%s, vals=%s\n", pts, nvals)
return pts.size
end
}
# nxts.merge!(news)
merge(nxts, news, memo)
}
# p nxts
$Memo << nxts
end
end
# main
while line = gets
line.strip!
next if line.empty?
n = line.to_i
$Memo << {[0] => [n]}
p solve(n)
end
解説
難しいと思います。
考え方
真上の点を0とします(問題の図では1になっています)。
そこから1〜(n-1)の場所に目盛を振ります。
それで、1〜nの長さを全て測れなければ、1回前に振った目盛よりも大きい場所に目盛を振り、また全ての長さを測れるかをチェックします。
これを最大n-1回行い、最小の回数で全ての長さを測れる目盛位置を見つけた時点で処理をやめれば良いわけです。
目盛を1箇所振るごとに計測できる長さは、新たに振った目盛とそれまでに存在する目盛のどれかを選んだ場合で、時計回りと反時計回りで2パターン増えます。
また、前回振った目盛位置よりも大きい目盛位置がない場合、無視します。これである程度重複を削除できます。
n=4で具体的にやってみます。
初期状態:目盛位置[0]=>測れる長さ[4]
1回目:
1に目盛を振る:[0,1]=>[1,3,4]
2に目盛を振る:[0,2]=>[2,4]
3に目盛を振る:[0,3]=>[1,3,4]
2回目:
[0,1]=>[1,3,4]に対して
2に目盛を振る:[0,1,2]=>[1,2,3,4]……(*)
3に目盛を振る:[0,1,3]=>[1,3,4]
(*)で答えに到達したのでここでやめるが、以下は説明のため処理を記述
[0,2]=>[2,4]に対して
3に目盛を振る:[0,2,3]=>[1,2,3,4]
[0,3]=>[1,3,4]に対して
4以上の目盛は触れないので無視
と言う具合に答えを求めることができます。
ただし、問題は高速化です。上記のロジックを実装しただけではRubyの場合、n=30の時に10秒以上かかってしまいました。
具体例で目につくのが1回目の処理でできた結果のうち[0,1]=>[1,3,4]と[0,3]=>[1,3,4]です。この2つは測れる長さのパターンが同じなので、より小さい目盛を刻んでいる(目盛を振れなくなって無視される可能性が低い)[0,1]=>[1,3,4]だけを残せばうまくゆきそうです。
この例ではnが小さいので問題になりませんが、1回の操作あたり生成されるパターン数が約1/2になるのは大きいので、測れる長さが同じになるパターンは目盛位置が最も小さいものを残して、それ以外を捨てることにしました。
これでn=30の場合でも1秒を切ることができます。
main
$Memoは1〜(n-1)回目の操作でできたパターンを操作回数を添字として{[目盛位置, ...] => [測れる長さ, ...]}の形式の連想配列で保持します。
初期値は0の場所だけに目盛が振られた状態で測れる長さはnなので{[0]=>[n]}を初期値として保持します。
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n)
問題を解きます。
checkerは正解時の測れる長さのリストで[1,2,...,n]と言う配列です。
45〜67行目のループは目盛を振る操作です。
46行目で前回の操作結果をlastsに保持します。
nxtsは今回の操作でできたパターンを保持する領域です。
memoは測れる長さが同じパターンを排除するために使用します。
lastsの要素を順次取り出し、add()に渡して新しい目盛を振ります。add()は振ることのできる目盛を振った全パターンを返すのでそれをnewsに取ります。
newsのパターンを1つずつ取り出し、測れる長さがchackerと同じかを調べます。もし同じものがあれば答えを見つけたので、目盛位置の数を返却して終わります。
そうでなければmerge()関数でnxtsにnewsをマージして次回の操作のために結果を保持します。
1回の操作が全て終了して答えに達しなかったら$Memoにnxtsを保持し、次の操作に移ります。
add(n, bef, vals)
目盛を1つ増やします。
目盛を振れる場所が複数ある場合は、その全てに振った場合のパターンを作成します。
引数nは入力値、befは前回の目盛位置、valsは前回の目盛位置で測れる長さのパターンです。
retは返却値の連想配列で{[目盛位置, ...] => [測れる長さ, ...]}の形式です。
19〜25行目のパターンで前回振った目盛位置+1〜(n-1)までの場所に目盛を振ります。
20行目が目盛位置の追加です。
21行目でaddVals()を呼び、新たに追加した目盛位置によって増えた測定可能な長さを追加します。
22行目の処理は測定可能な長さをソートするとともに、同じ長さをリストから削除します。
retに結果を追加します。
全ての目盛位置に目盛を追加したらretを返却します。
addVals(n, bef, i)
新たに追加した目盛位置によって測定可能になった長さのリストを求めます。
引数nは入力値、befは目盛追加前の目盛位置のリスト、iは追加する目盛位置です。
retは目盛iを追加したことによって測定可能になった長さのリストです。
元の目盛位置を順次選び、iとの差がその2つの目盛間で測れる長さになります。9行目は時計回り、10行目は反時計回りに測った時の長さになります。
新たに測定可能な長さのリストを返却します。
merge(to, from, memo)
引数toの連想配列にfromの連想配列をマージします。
memoは同じ測定可能な長さのリストを持っているものを無視するため、{[測定可能な長さ, ...] => true}と言う形式の連想配列です。
fromの要素を1つずつ取り出します。
memoに測定可能な長さのリストが一致するものがあれば無視します。
toに全く同じ目盛位置のリストがあれば無視します。
toにfromの値を追加します。
追加した要素の測定可能な長さのリストをmemoに保持します。
追加した結果のtoを返却します。
雑感
プログラムを考えているときは再起だとうまくできない気がしていましたが、この文章を書いている間に再起でもうまくできるような気がしてきました。
あと、測れる長さのリストはビットフラグにした方がよかったかな、と思います。重複削除とソートが必要ないし、答えに達したかのチェックも速いし。目盛位置の方もビットフラグにできるけど、ビットが立っている位置を毎回求めないといけないのであまりお得感が無いように思えますがどうなんでしょう?