CodeIQ:半径が同じ円を重ならないように描く
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「半径が同じ円を重ならないように描く」(CodeIQ)を参照してください。
問題の概要
座標平面において、x軸上の点を中心とする円をいくつか描くことを考えます。
ただし、中心となるx軸上の点のx座標はいずれも m 以下の「素数」とします。
これらの点の中から中心とする点を n 個選び、直径が同じ円を描くとき、いずれの円も重ならないようにします。
(円が外接するときは問題ないものとします)
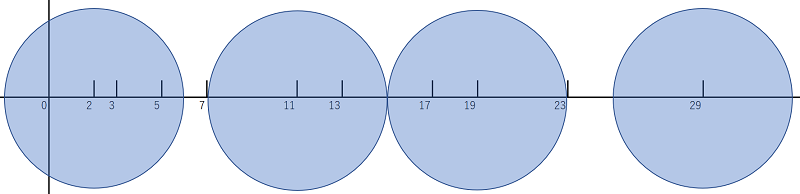
例えば、m = 30, n = 4 のとき、以下の位置を中心にする円を描くと、いずれの円も重なりません。
中心:(2, 0), (11, 0), (19, 0), (29, 0)
この条件を満たす円を描いたとき、直径が最大になるのは上記の図のときで、その直径は8です。
標準入力から m と n が与えられたとき、直径が最大となる場合を求め、その「直径」を標準出力に出力してください。
なお、m, n はいずれも正の整数とし、m < 1,000,000を満たすものとします。
【入出力サンプル】
標準入力
30 4
標準出力
8
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
require 'prime'
$Primes = nil
def search(st, r)
for i in (st+1)...$Primes.size
return i if $Primes[i] >= ($Primes[st] + r)
end
return -1
end
def checkNext(now, r, cnt)
# printf("%d - %d = %d, r*cnt=%d\n", $Primes.last, $Primes[now], $Primes.last - $Primes[now], r * cnt)
return false if(($Primes.last - $Primes[now]) < r * cnt)
return true
end
def check(r, n)
# printf("r=%d, n=%d\n", r, n)
now = 0
(n-2).downto(1){|cnt|
now = search(now, r)
# p $Primes[now]
return false if now < 0
return false if !checkNext(now, r, cnt)
}
return true
end
def solve(m, n)
$Primes = Prime.each(m).to_a
max_r = ($Primes.last - $Primes.first) / (n-1)
max_r.downto(1){|r|
return r if check(r, n)
}
end
# main
while line = gets
line.strip!
next if line.empty?
m,n = line.split.map{|a| a.to_i}
p solve(m, n)
end
解説
問題を読んだ時に、円の外周の座標が整数になる必要があるかが分かりませんでした。何も書いていないので小数になる場合でも良いのだろうと言うことでやりましたが、それで問題なかった様です。
考え方
私の実装はシンプルです。
まず、m以下の素数のリストを生成します。
最大の半径の最初の候補を(m以下の最大の素数-2)/(n-1)とします。
これは、一番左の円の中心を2、一番右の円の中心をm以下の最大の素数とした場合の半径です。一番左の円の左半分と一番右の円の右半分は最大と最小の素数の外側になるので丁度円1つ分だけ減らせば、全ての円が隣接した状態になります。
後は、順番に円の中心を求めてゆきます。
次の円の中心は現在の円の中心に直径を足した座標以上で最小の素数になります。
これを繰り返して範囲内に収まらなかったら直径を1減らしてやり直す、を繰り返し、収まった時点の直径が答えになります。
計算量を減らすため、1つ右側の円に進むごとに範囲内に収まるかどうかをチェックします。範囲内に収まるためには(範囲内の最大の素数-現在の中心)が(直径*(残りの円の数-1))以下かどうかを調べればOKです。
例の図の場合だと次の様になります。
まず、最初の直径の候補は(29-2)/3=9です。
2つ目の円の中心は2+9=11以上の最小の素数なので11です。
29-11=18で残りの円は3個です。なので9*(3-1)=18と比較するとまだ大丈夫です。
3個目の円の中心は11+9=20以上の最小の素数なので23。29-23=6で、これは(残りの円の数-1)*直径=9より小さくなってしまいました。
なので、直径を8にしてやり直します。
今度は2つ目の円の中心は2+8=10から11。29-11 > 8*(3-1)なのでOK。
3つ目の円の中心は11+8=19。29-19 > 8*(2-1)なのでOK。
4つ目の円の中心は19+8=27から29。これが最後の円なので収まりました。
答えは8になります。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(m, n)
範囲内の素数のリストを生成し$Primesに保持します。
max_rは最初の直径候補です。
max_rから1まで直径を減らしながらcheck()の結果がtrueになるまで調べます。check()の結果がtrueの時のrを答えとして返却します。
check(r, n)
1つ目の円の中心は2と決め打っているので、2つ目の円から順番に中心座標を求め、全部の円の中心が範囲内にあるかを調べます。
引数rは直径、nは円の個数(入力値)です。
n-2から1まで円の個数を減らしながら調べます。n-2からなのは最初の座標が2と決まっているので2個目から開始すれば良いからです。
nowは中心となる素数の$Primesの要素番号です。
search()は次の中心の座標をとなる素数の要素番号を返します。
search()は範囲内の素数を中心座標にできなかった場合に-1を返すので、search()の結果が負数なら範囲内に収まらなかったということでfalseを返却します。
checkNext()は中心座標(となる素数の要素番号)と直径と残りの円の数-1から範囲内に円が収まるかを判定します。
checkNext()がfalseを返した場合、全ての円が収まりきらないのでfalseを返却します。
1までループして全てのチェックを通ったら全ての円が収まったのでtrueを返却します。
search(st, r)
次の円の中心座標を探します。
stは現在の円の中心座標となる素数の要素番号、rは直径です。
次の素数から始めて、現在の中心座標+r以上の素数になるまで$Primesを順番に調べます。
現在の中心座標+r以上の素数になった時点でその時の要素番号を返却します。
最後まで見つからなかったら-1を返却します。
checkNext(now, r, cnt)
現在の中心座標、直径、残りの円の個数-1から範囲内に残りの全ての円が収まるかを調べます。
nowは現在の円の中心の座標(の$Primesの要素番号)です。
rは直径です。
cntは残りの円の数-1です。
考え方に書いた通り、最後の素数-現在の中心座標と直径*(残りの円の数-1)を比較し、最後の素数-現在の中心座標の方が小さいならfalse、そうでなければtrueを返します。
雑感
時間的に大丈夫かな? と思うところが2つありましたが大した工夫をしなくてもOKでした。
一つは素数のリストを作っていて間に合うかでしたが、1,000,000以下の素数列挙をやってみたらローカルで0.18秒だったので、これは一旦列挙してしまってOKとなりました。
もう一つは次の中心候補を求めるのですが、二分探索を応用するとかして高速化する必要があるかな? と思いましたが、まぁ単純に線形探索でやってみてダメだったら対応しようと思ってやってみたらうまく行きました。
結果的に、円を1個増やすごとに残りが収まるかのチェックだけで済んだので、割と簡単にできたという印象です。