CodeIQ：崩れないように積み上げて！

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「崩れないように積み上げて！」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
直方体の箱を重ねて置くことを考えます。
ただし、上の箱は下の箱よりも小さくないと、崩れてしまう可能性があります。
そこで、大きな箱の上に小さな箱を置くことを考えます。

ここで「小さい」とは縦と横の長さがともに短いことにします。
つまり、中央に重ねて置くと、上から見たときに下の箱の輪郭が見えるようにします。
また、箱は縦か横方向に綺麗に置くものとし、斜めに傾けて置くことはありません。

m 個の箱を用意したとき、その上面の面積の和が n でした。
このような箱のサイズの組み合わせが何通りあるか求めてください。
ただし、辺の長さはいずれも正の整数とし、箱の高さは考えないものとします。
なお、同じサイズの箱でも縦と横の置き方が違う場合は別々にカウントします。

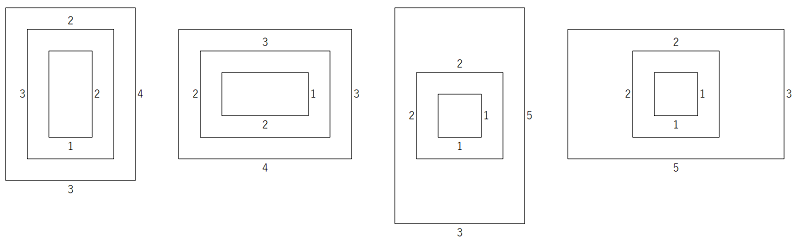
例えば、m = 3, n = 20 のとき、上から見ると以下の4通りがあります。


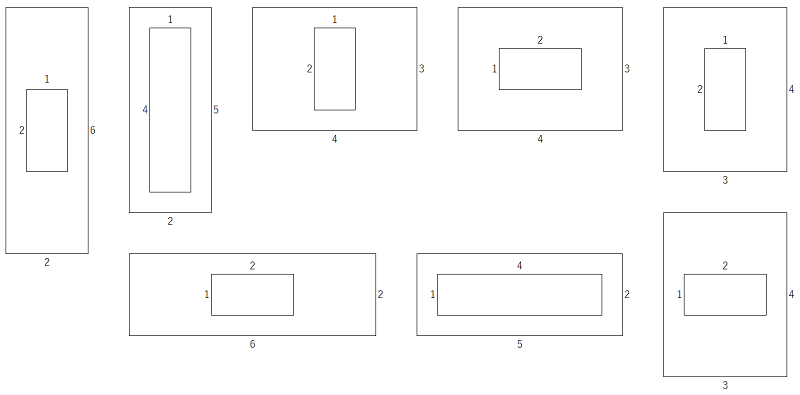
同様に、m = 2, n = 14 のとき、上から見ると以下の8通りがあります。


標準入力から m, n が与えられたとき、その箱のサイズの組み合わせを求め、その数を標準出力に出力してください。
なお、m, n は 0 < m < n < 250を満たす整数とします。

【入出力サンプル】
標準入力
3 20

標準出力
4

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

def getNext(m, n, x, y)
#	printf("m=%d, n=%d, x=%d, y=%d\n", m, n, x, y)
	return $Memo[[m,n,x,y]] if $Memo[[m,n,x,y]] != nil
	if m == 0 then
		if n == 0 then return 1
		else return 0
		end
	end

	ret = 0
	st = (m>1 ? 2 : 1)
	for nx in st...x
		for ny in st...y
			break if n < nx*ny
			ret += getNext(m-1, n-nx*ny, nx, ny)
		end
	end

	$Memo[[m,n,x,y]] = ret
	$Memo[[m,n,y,x]] = ret if x != y
	return ret
end

def solve(m, n)
	ret = 0
	st = (m>1 ? 2 : 1)
	for x in st..n
		y = st
		while x*y <= n
			ret += getNext(m-1, n-x*y, x, y)
			y += 1
		end
	end
	return ret
end

# main
while line = gets
	line.strip!
	next if line.empty?

	m,n = line.split.map{|a| a.to_i}
	p solve(m,n)
end

解説

分かりにくい問題ではありませんが、コードがごちゃっとしています。

考え方

基本的な考え方は単純です。
箱の縦横の長さを決め、一段上の箱はそれよりも縦横ともに1以上小さくします。
途中で縦か横の長さが0になった場合は無視します。
これを再帰的に行い、その度に縦*横（つまり面積）をnから引いてゆき、m回操作した時にn=0になっていればカウントを1増やし、そうでなければ無視すれば良いわけです。

後は高速化のためメモ化しますが、メモ化だけでは時間が足りませんでした。

なので、もう少し工夫します。
一つはメモするときに縦横の組み合わせとともに横縦（縦と横を入れ替えた場合）も同時にメモします。
もう一つは最小の辺の長さを大きくします。私のコードは入力値のmが1の時は1からそれ以外は2からにしていますが、後で考えたらもっと効率よくできます（雑感に書きます）。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(m, n)

一番下の箱はその下の箱が無く、縦横の辺の長さの制約が無いのでこれだけsolve()で列挙しています（よく考えたら特別扱いの必要はありませんでした。雑感に書きます）。

retは答えの数です。
stは辺の最小値でm=1の時は1を最小、それ以外の場合一番下の箱の辺に1はありえないので2以上にしています（これももっとうまくできます。雑感で書きます）。

後は横xと縦yの長さを任意に決め、その積がn未満の間getNext()で上の箱を積む処理を行います。getNext()は積めるパターン数を返すのでretに加算します。

最終的にretを返却します。

getNext(m, n, x, y)

mは後何回箱を積むかです。
nは残りm回箱を積んだ時、その箱の面積の合計です。
x,yは一つ下の箱の横と縦の長さです。

$Memoにパターンがあれば計算済みなので$Memoの値を返します。
mが0の時、nが0ならOKのパターンなので1を返します。nが0でなければNGなので0を返します。

stは最小の辺の長さでm=1の時以外は最小2、m=1の時は最小1とします。
後はst以上でy、x未満の範囲で任意に縦横の長さを決め、再帰的にgetNext()を呼び出します。

ret返却前に$Memoに結果をメモしますが、x,yを入れ替えたパターンも記録します。

雑感

まず、一番下の箱だけを特別扱いしましたが、よく考えたらnを辺の長さの上限にできたのでgetNext()と一つにできました。
後、最小の辺の長さは単純にmにできました。例えば3段積む時、一番上の箱の最小は1*1なので一番下は3*3以上でなければなりません。
もう少し考えればよかった、というより、コードを書いている時には何でこのくらいのことに気がつかなかったんだろう？