CodeIQ:展開図上の反対側
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「展開図上の反対側」(CodeIQ)を参照してください。
問題の概要
【概要】
マス目を6つ指定します。
6つのマス目を立方体の展開図として組み上げた場合に、最初の面の反対側がどの面になるのかを計算してください。
【入出力】
入力は
glkmnq
のようになっています。
区切り文字なしで、面を示すアルファベット(図を参照)が6つ並んでいます。
出力するのは、最初の面の反対側の面のアルファベットです。
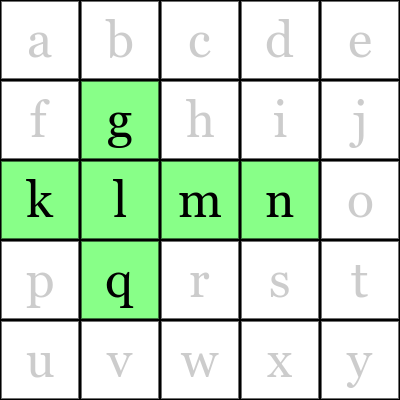
glkmnq
に対応する出力は、下図の通り、g の反対側は q なので
q
になります。
ただし、
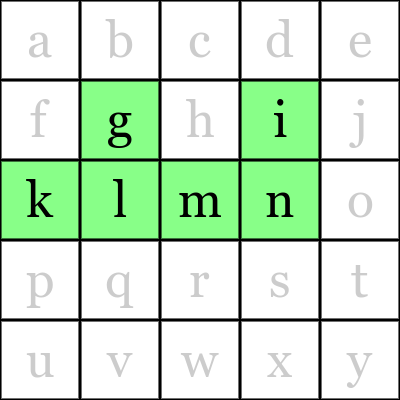
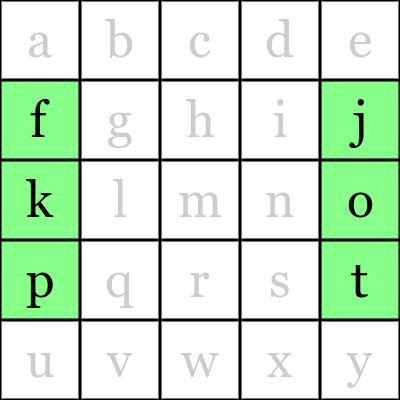
jotfkpやklmngi
のように、
入力が立方体の展開図をなしていない場合は
-
を出力してください。
【例】
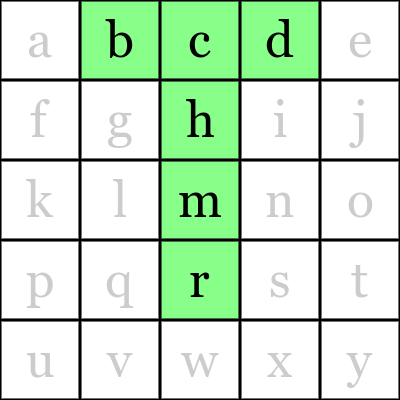
入力 出力 図 glkmnq q klmngi - jotfkp - bcdhmr d
【補足】
不正な入力に対処する必要はありません。
ひとつながりになっていない場合は、展開図にはなっていないと判断してください。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
PATTERN = [
{"seq" => [0, 1, 2, 6, 11, 16], "rev" => {0=>2, 2=>0, 1=>11, 11=>1, 6=>16, 16=>6}},
{"seq" => [0, 1, 6, 7, 11, 16], "rev" => {0=>7, 7=>0, 1=>11, 11=>1, 6=>16, 16=>6}},
{"seq" => [0, 1, 6, 11, 12, 16], "rev" => {0=>12, 12=>0, 1=>11, 11=>1, 6=>16, 16=>6}},
{"seq" => [0, 1, 6, 11, 16, 17], "rev" => {0=>17, 17=>0, 1=>11, 11=>1, 6=>16, 16=>6}},
{"seq" => [0, 1, 4, 5, 10, 15], "rev" => {0=>10, 10=>0, 1=>9, 9=>1, 5=>15, 15=>5}},
{"seq" => [0, 4, 5, 6, 10, 15], "rev" => {0=>10, 10=>0, 6=>9, 9=>6, 5=>15, 15=>5}},
{"seq" => [0, 4, 5, 10, 11, 15], "rev" => {0=>10, 10=>0, 11=>9, 9=>11, 5=>15, 15=>5}},
{"seq" => [0, 4, 5, 10, 15, 16], "rev" => {0=>10, 10=>0, 16=>9, 9=>16, 5=>15, 15=>5}},
{"seq" => [0, 1, 5, 9, 10, 15], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 9=>1, 1=>9}},
{"seq" => [0, 5, 6, 9, 10, 15], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 9=>6, 6=>9}},
{"seq" => [0, 5, 9, 10, 11, 15], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 9=>11, 11=>9}},
{"seq" => [0, 5, 9, 10, 15, 16], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 9=>16, 16=>9}},
{"seq" => [0, 1, 5, 10, 14, 15], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 14=>1, 1=>14}},
{"seq" => [0, 5, 6, 10, 14, 15], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 14=>6, 6=>14}},
{"seq" => [0, 5, 10, 11, 14, 15], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 14=>11, 11=>14}},
{"seq" => [0, 5, 10, 14, 15, 16], "rev" => {0=>10, 10=>0, 5=>15, 15=>5, 14=>16, 16=>14}},
# -----
{"seq" => [0, 5, 6, 7, 8, 10], "rev" => {0=>10, 10=>0, 5=>7, 7=>5, 6=>8, 8=>6}},
{"seq" => [0, 5, 6, 7, 8, 11], "rev" => {0=>11, 11=>0, 5=>7, 7=>5, 6=>8, 8=>6}},
{"seq" => [0, 5, 6, 7, 8, 12], "rev" => {0=>12, 12=>0, 5=>7, 7=>5, 6=>8, 8=>6}},
{"seq" => [0, 5, 6, 7, 8, 13], "rev" => {0=>13, 13=>0, 5=>7, 7=>5, 6=>8, 8=>6}},
{"seq" => [0, 4, 5, 6, 7, 9], "rev" => {0=>9, 9=>0, 4=>6, 6=>4, 5=>7, 7=>5}},
{"seq" => [0, 4, 5, 6, 7, 10], "rev" => {0=>10, 10=>0, 4=>6, 6=>4, 5=>7, 7=>5}},
{"seq" => [0, 4, 5, 6, 7, 11], "rev" => {0=>11, 11=>0, 4=>6, 6=>4, 5=>7, 7=>5}},
{"seq" => [0, 4, 5, 6, 7, 12], "rev" => {0=>12, 12=>0, 4=>6, 6=>4, 5=>7, 7=>5}},
{"seq" => [0, 3, 4, 5, 6, 8], "rev" => {0=>8, 8=>0, 3=>5, 5=>3, 4=>6, 6=>4}},
{"seq" => [0, 3, 4, 5, 6, 9], "rev" => {0=>9, 9=>0, 3=>5, 5=>3, 4=>6, 6=>4}},
{"seq" => [0, 3, 4, 5, 6, 10], "rev" => {0=>10, 10=>0, 3=>5, 5=>3, 4=>6, 6=>4}},
{"seq" => [0, 3, 4, 5, 6, 11], "rev" => {0=>11, 11=>0, 3=>5, 5=>3, 4=>6, 6=>4}},
{"seq" => [0, 2, 3, 4, 5, 7], "rev" => {0=>7, 7=>0, 2=>4, 4=>2, 3=>5, 5=>3}},
{"seq" => [0, 2, 3, 4, 5, 8], "rev" => {0=>8, 8=>0, 2=>4, 4=>2, 3=>5, 5=>3}},
{"seq" => [0, 2, 3, 4, 5, 9], "rev" => {0=>9, 9=>0, 2=>4, 4=>2, 3=>5, 5=>3}},
{"seq" => [0, 2, 3, 4, 5, 10], "rev" => {0=>10, 10=>0, 2=>4, 4=>2, 3=>5, 5=>3}},
# ---
{"seq" => [0, 1, 2, 7, 8, 9], "rev" => {0=>2, 2=>0, 1=>8, 8=>1, 7=>9, 9=>7}},
{"seq" => [0, 1, 2, 3, 4, 5], "rev" => {0=>2, 2=>0, 1=>4, 4=>1, 3=>5, 5=>3}},
{"seq" => [0, 5, 9, 10, 14, 19], "rev" => {0=>10, 10=>0, 5=>14, 14=>5, 9=>19, 19=>9}},
{"seq" => [0, 5, 9, 11, 16, 21], "rev" => {0=>10, 10=>0, 5=>16, 16=>5, 11=>21, 21=>11}},
#---
{"seq" => [0, 1, 6, 7, 8, 11], "rev" => {0=>7, 7=>0, 1=>11, 11=>1, 6=>8, 8=>6}},
{"seq" => [0, 3, 4, 5, 9, 14], "rev" => {0=>9, 9=>0, 3=>5, 5=>3, 4=>14, 14=>4}},
{"seq" => [0, 3, 4, 5, 10, 11], "rev" => {0=>10, 10=>0, 3=>5, 5=>3, 4=>11, 11=>4}},
{"seq" => [0, 5, 9, 10, 11, 14], "rev" => {0=>10, 10=>0, 5=>14, 14=>5, 9=>11, 11=>9}},
{"seq" => [0, 5, 6, 7, 9, 10], "rev" => {0=>10, 10=>0, 5=>7, 7=>5, 6=>9, 9=>6}},
{"seq" => [0, 5, 9, 10, 11, 16], "rev" => {0=>10, 10=>0, 5=>16, 16=>5, 9=>11, 11=>9}},
{"seq" => [0, 1, 3, 4, 5, 10], "rev" => {0=>10, 10=>0, 3=>5, 5=>3, 1=>4, 4=>1}},
{"seq" => [0, 5, 6, 7, 11, 16], "rev" => {0=>11, 11=>0, 5=>7, 7=>5, 6=>16, 16=>6}},
# ---
{"seq" => [0, 1, 6, 7, 8, 12], "rev" => {0=>7, 7=>0, 1=>12, 12=>1, 6=>8, 8=>6}},
{"seq" => [0, 4, 5, 8, 9, 14], "rev" => {0=>9, 9=>0, 8=>5, 5=>8, 4=>14, 14=>4}},
{"seq" => [0, 4, 5, 6, 11, 12], "rev" => {0=>11, 11=>0, 4=>6, 6=>4, 5=>12, 12=>5}},
{"seq" => [0, 5, 6, 9, 10, 14], "rev" => {0=>10, 10=>0, 5=>14, 14=>5, 9=>6, 6=>9}},
{"seq" => [0, 4, 5, 6, 8, 9], "rev" => {0=>9, 9=>0, 4=>6, 6=>4, 5=>8, 8=>5}},
{"seq" => [0, 4, 5, 10, 11, 16], "rev" => {0=>10, 10=>0, 5=>16, 16=>5, 4=>11, 11=>4}},
{"seq" => [0, 1, 3, 4, 5, 9], "rev" => {0=>9, 9=>0, 3=>5, 5=>3, 1=>4, 4=>1}},
{"seq" => [0, 5, 6, 11, 12, 16], "rev" => {0=>11, 11=>0, 5=>12, 12=>5, 6=>16, 16=>6}},
# ---
{"seq" => [0, 1, 6, 7, 8, 13], "rev" => {0=>7, 7=>0, 1=>13, 13=>1, 6=>8, 8=>6}},
{"seq" => [0, 4, 5, 9, 13, 14], "rev" => {0=>9, 9=>0, 13=>5, 5=>13, 4=>14, 14=>4}},
{"seq" => [0, 5, 6, 7, 12, 13], "rev" => {0=>12, 12=>0, 5=>7, 7=>5, 6=>13, 13=>6}},
{"seq" => [0, 1, 5, 9, 10, 14], "rev" => {0=>10, 10=>0, 5=>14, 14=>5, 9=>1, 1=>9}},
{"seq" => [0, 3, 4, 5, 7, 8], "rev" => {0=>8, 8=>0, 3=>5, 5=>3, 4=>7, 7=>4}},
{"seq" => [0, 1, 6, 11, 12, 17], "rev" => {0=>12, 12=>0, 1=>11, 11=>1, 6=>17, 17=>6}},
{"seq" => [0, 1, 3, 4, 5, 8], "rev" => {0=>8, 8=>0, 3=>5, 5=>3, 1=>4, 4=>1}},
{"seq" => [0, 5, 6, 11, 16, 17], "rev" => {0=>11, 11=>0, 5=>17, 17=>5, 6=>16, 16=>6}},
# ---
{"seq" => [0, 1, 6, 7, 12, 13], "rev" => {0=>7, 7=>0, 1=>12, 12=>1, 6=>13, 13=>6}},
{"seq" => [0, 4, 5, 8, 9, 13], "rev" => {0=>9, 9=>0, 4=>13, 13=>4, 5=>8, 8=>5}},
{"seq" => [0, 1, 4, 5, 8, 9], "rev" => {0=>9, 9=>0, 1=>4, 4=>1, 5=>8, 8=>5}},
{"seq" => [0, 5, 6, 11, 12, 17], "rev" => {0=>11, 11=>0, 5=>12, 12=>5, 6=>17, 17=>6}},
]
def isConnected(line)
map = [
['a', 'b', 'c', 'd', 'e'],
['f', 'g', 'h', 'i', 'j'],
['k', 'l', 'm', 'n', 'o'],
['p', 'q', 'r', 's', 't'],
['u', 'v', 'w', 'x', 'y'],
]
dir = [[-1, 0], [0, 1], [1, 0], [0,-1]]
position = {}
for i in 0...5
for j in 0...5
position[map[i][j]] = [i,j]
end
end
arr = line.split("")
queue = [arr.shift]
while !queue.empty?
c = queue.pop
pos = position[c]
for d in dir
nr = pos[0]+d[0]
nc = pos[1]+d[1]
next if (nr < 0) || (nc < 0) || (5 >= nr) || (5 >= nc)
del = arr.delete(map[nr][nc])
queue.push(del) if del != nil
end
end
return arr.empty?
end
def solve(line)
cube = line.sort
seq = cube.map{|a| a.ord - cube[0].ord}
for ptn in PATTERN
if seq == ptn["seq"] then
face = line[0].ord - cube[0].ord
back = ptn["rev"][face]
return (cube[0].ord + back).chr
end
end
return "-"
end
# main
while line = gets
line.strip!
next if line.empty?
if isConnected(line) then
cube = line.split("")
puts solve(cube)
else
puts '-'
end
end
解説
★★★の問題です。
難しいです。私はうまいやり方が分からなかったので力技でやりました。
多分、もっとうまい方法があります。
考え方
展開図のパターンと表裏になる面の対応を定数化し、全パターンをチェックして裏面を求めるという力技です。
パターンは入力される文字をソートし、文字コードが一番小さい文字を0番目とした時に、その他の文字が何番目になるかを配列にしたものです。一番小さい文字からの相対値にすることで上下左右にずれた場合でもチェックできます。
ちなみに、回転したり反転した時の図形も何も考えずにパターン化しています(64通りになります)。
表裏の対応も、文字コードが一番小さい文字からの相対値です。得られた値に入力値の最も文字コードが小さい文字の文字コードを加え、文字コードから文字に変換すれば答えになります。
この方法だと、「ejotda」のようなパターンを展開図としてしまうので、全てのマス目が繋がっているかを別途チェックしています。
これは次のようにしてできます。
入力値の最初の文字を入力値から削除してキューに入れます。
キューから1文字取り出し、隣接する文字を調べます。
その文字に隣接する文字があったら入力値から削除します。同時にキューに追加します。
これをキューが空になるまで繰り返した結果、入力値に1文字も残っていなかったら全部が繋がっています。
main
定数PATTERNは回転や反転を含めて、展開図のパターンと各面の表裏の対応を列挙したものです。
"seq"が展開図のパターンで、展開図のうち最も小さい文字を0、その他の文字はそこから何番目かで表しています。
"rev"はある面とその裏面の対応を連想配列にしたものです。
isConnected()で入力値が全部繋がっているかをチェックします。
繋がっていたらsolve()に渡して、問題を解きます。
繋がっていないときは'-'を印字します。
isConnected(line)
入力値がひとつながりになっているかをチェックします。
mapは盤面を表す定数です。
dirは上下左右の相対座標です。
positionは各文字がどの座標にあるかを示すもので、88〜92行目でmapから生成します。
94行目で入力値lineを配列にし、95行目で先頭の文字を取り出してqueueに入れます。
97〜108行目のループでqueueが空になるまで探索します。
queueの最後の要素を取り出し、その座標を得ます。
その上下左右の文字を得たら、それがarrにあるかをチェックして、あったらarrから削除すると同時にqueueに追加します。
ループが終了した時にarrが空なら全部が繋がっていますし、そうでなければどこかで切れています。
solve(a, b)
入力値をソートし、文字コードに直して入力値の最も小さい値からの相対番号にします(114〜115行目)。
PATTERNにseqと同じものがあるかをチェックし、同じものがあったら入力値の先頭の文字の相対番号の裏側の文字の相対番号を得ます。
それに最も小さい文字の文字コードを加えてから文字に戻し、返却します。
PATTERNに一致するものがなければ'-'を返却します。
雑感
我ながらこれは頭が悪いと思います。
多分、各面の隣接面を求めることで上手くやれそうなのですが……。
例えばglkmnqの場合だと、
g:[k,l,m,n]
k:[g,l,q,n]
l:[g,k,m,q]
m:[g,l,n,q]
n:[g,k,m,q]
q:[k,l,m,n]
と自分と裏面以外の4面が隣接します。立方体の展開図だと各文字にそれぞれ4ずつの文字が隣接面となり、隣接面の文字を全て集めると各文字が4個ずつになるので、そうならないときはダメなパターンと判定できるのではないかと思うのですが。
でも、隣接面を求める方法が分かりませんでした。