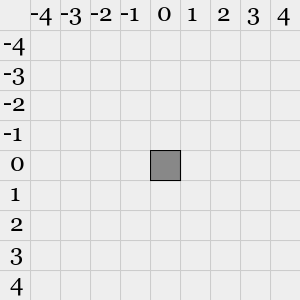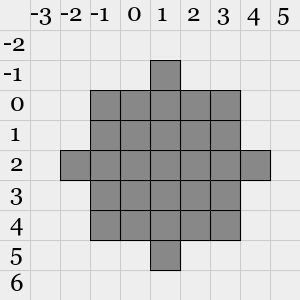CodeIQ:ドット絵の丸が2つ
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「ドット絵の丸が2つ」(CodeIQ)を参照してください。
問題の概要
【概要】
マス目に沿った、円のような形を2つ指定します。
両者に含まれるマスの数を計算してください。
【入出力】
入力は
1,2,3 4,5,4
のようになっています。
空白区切りで2つの図形が並んでいます。
各図形は、コンマ区切りで 中心のx座標、中心のy座標、半径 をならべたものです。
マス目の中心と中心の距離が、半径以下のマスが図形に含まれます。
具体的には下表のとおりです:
図形を表す記号 図形 0,0,0 1,2,3 4,5,6
出力は、普通に10進数です。
2つの図形の両方に含まれるマスの数を答えてください。
1,2,3 4,5,4
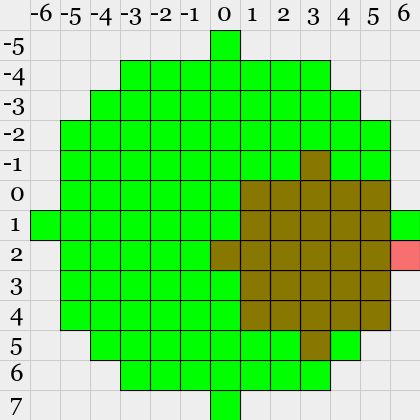
に対応する出力は、下図の通り、
10になります。
【例】
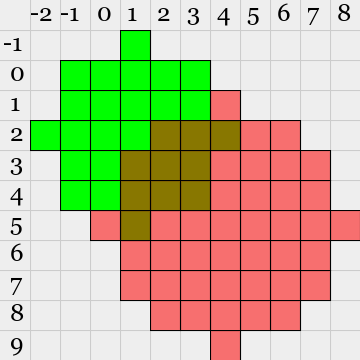
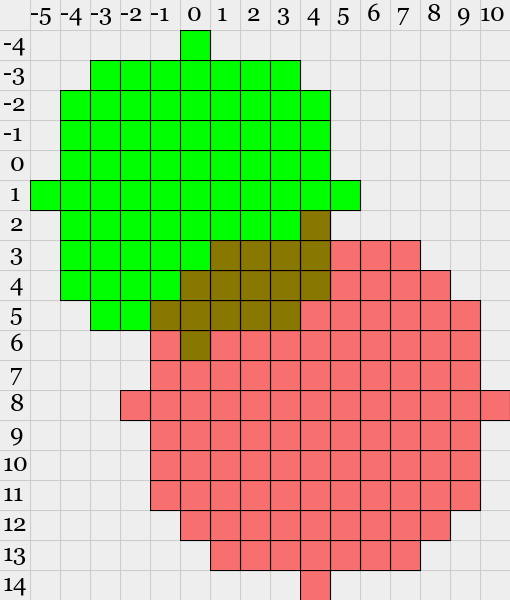
入力 出力 図 1,2,3 4,5,4 10 0,1,5 4,8,6 16 0,1,6 3,2,3 28
【補足】
不正な入力に対処する必要はありません。
中心座標は 0以上一万以下です。
半径の値は 0以上一万以下です。
中心座標・半径は、いずれも0以上の整数ですが、マス目はマイナスの座標にもあります。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def points(x, y, r)
ret = {y => [x-r, x+r]}
for i in 1..r
q = Math.sqrt(r**2 - i**2).floor
ret[y+i] = [x-q, x+q]
ret[y-i] = [x-q, x+q]
end
return ret
end
def count(a, b)
return 0 if a[1] < b[0]
return 0 if a[0] > b[1]
l = (a[0] >= b[0] ? a[0] : b[0])
r = (a[1] <= b[1] ? a[1] : b[1])
return r-l+1
end
def solve(a, b)
pas = points(a[0], a[1], a[2])
pbs = points(b[0], b[1], b[2])
ret = 0
for y in (a[1]-a[2])..(a[1]+a[2])
next if pbs[y] == nil
ret += count(pas[y], pbs[y])
end
return ret
end
# main
while line = gets
line.strip!
next if line.empty?
a, b = line.split.map{|l| l.split(',').map{|v| v.to_i}}
if a[2] <= b[2] then p solve(a,b)
else p solve(b,a)
end
end
解説
結構難しそうですが、以外にそうでもありません。
考え方
まず、中心から右下の1/4の扇型の円周部分の座標を考えます。
中心座標を(x,y)としてy座標を1ずつ半径まで増やした場合、x座標はx+√(r2-i2)になります(1≦i≦y)。
ややこしいことを考えず、Math.sqrtで浮動小数点で座標を求め、floorで端数を切り捨てると中心を含む座標になります。
左下の座標はx-√(r2-i2)になり、上方向はy座標がy-iになるだけで、x座標は下側と同じになるので、右下方向だけを計算すれば同時に求められます。
2つの円について同じ操作を行えばそれぞれの円の境界座標のリストを作ることができます。
後は重なっている部分です。
小さい方の円を基準に重なっている部分を調べます。
次の場合は円が重なっていません。
小さい方の円のy座標に大きい方の円のy座標が無い。
あるy座標の小さい方の円の右側のx座標が大きい方の円の左側のx座標より小さい。
あるy座標の小さい方の円の左側のx座標が大きい方の円の右側のx座標より大きい。
それ以外の場合は重なっています。
重なっている部分の両端のx座標は、
小さい方の円の左のx座標が大きい円の左のx座標以上なら、小さい方の円の左のx座標が重なっている部分の左側の座標、そうでなければ大きい方の円の左のx座標が重なっている部分の左側です。
小さい方の円の右のx座標が大きい円の右のx座標以下なら、小さい方の円の右のx座標が重なっている部分の右側の座標、そうでなければ大きい方の円の右のx座標が重なっている部分の右側です。
これで重なっている部分の左右のx座標がわかるので、各y座標についてその差+1が重なっている領域の数になります。
なので、小さい方の円の各y座標について重なっている部分を足し合わせれば答えになります。
main
入力値を数値にし、それぞれをsolve()に渡し、結果を印字します。
小さい方の円を基準にするため半径を比較して小さい方をsolve()の第一引数、大きい方を第二引数に指定します。
solve(a, b)
aは小さい方の円、bは大きい方の円の[中心x座標, 中心y座標, 半径]です。
それぞれの円についてpoints()で{y座標 => [左のx座標, 右のx座標]}の連想配列を求めます。
小さい方の円のy座標の最小値から最大値までループし、重なり部分をcount()で求め、結果を加算します。30行目は小さい方の円のy座標に大きい方の円が無い場合なので無視します。
最終的にretが答えなのでそれを返却します。
points(x, y, r)
考え方に書いた通り、円のy座標の中心から上下のy座標まで、各y座標の左右のx座標を求めます。
y座標が中心にあるときはx座標はx+rとx-rなのでretの初期値とします。
qは考え方に書いた通りfloor(√(r2-i2))です。
これを下側(y+i)と上側(y-i)について[x+q, x-q]とすれば左右のx座標が計算できます。
count(a, b)
aとbはそれぞれあるy座標における、小さい方の円の左右のx座標と大きい方の円の左右のx座標です。
16〜17行目は円が重なっていない場合なので重なり部分0で戻ります。
19〜20行目で重なり部分の左側と右側のx座標を求めます。
l-r+1があるy座標の重なり部分なのでそれを返却します。
雑感
問題を読んだ時、高速化のためにはビル・アトキンソンがQuickDrawでやった方法を使う必要があるのかな、と思って調べたら結構工夫しないと単純に浮動小数点で計算した方が早いらしかったので、やってみたら十分間に合いました。
高速化に特に工夫がいらないのであれば単純な問題だと思います。