CodeIQ：スイッチを反転しても同じ数だけ点灯する？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「スイッチを反転しても同じ数だけ点灯する？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
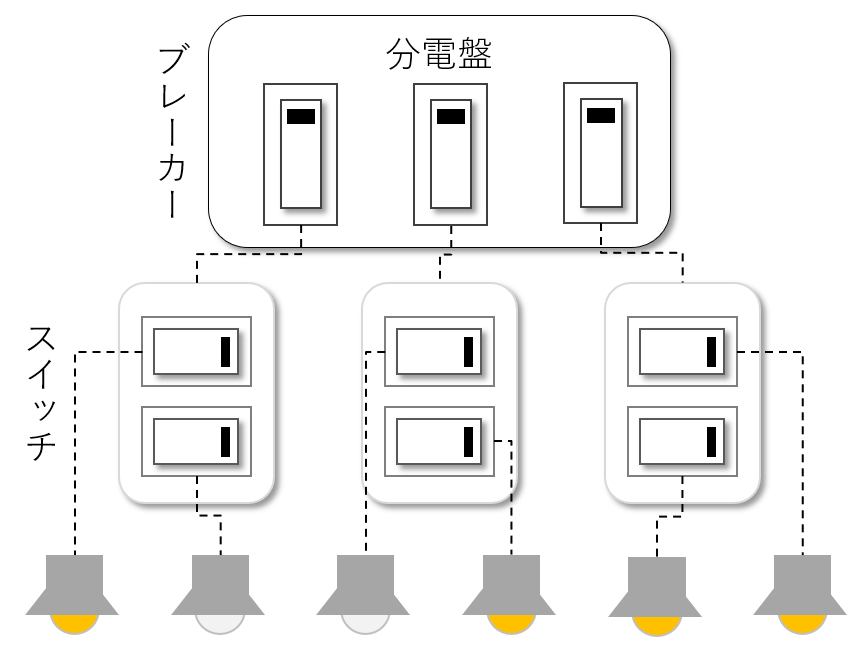
家庭に必ずある分電盤。その中にはブレーカーがあり、家庭内の電気スイッチやコンセントなどにつながっています。
ここでは、1つのブレーカーが2つのスイッチにつながっているものとします。
また、それぞれのスイッチに対して電球が1つずつ付いています。



スイッチをONにしても、そのスイッチにつながるブレーカーでONになっていないと電球は点灯しません。
もちろん、ブレーカーがONになっていても、スイッチがONになっていないと電球は点灯しません。

今、m 個のブレーカーがあり、n 個の電球が点灯しています。
ここで、すべてのスイッチを反転させたとき、点灯している電球の数が同じでした。
(あくまでもスイッチ部分の反転のみで、ブレーカーを触ることはありません。)
このようなブレーカー、スイッチの状態が何通りあるか求めます。

例えば、m = 2, n = 1 のとき、以下のような16通りがあります。
(色が付いている部分が点灯している部分)

ブレーカー1 スイッチ1-1 スイッチ1-2 ブレーカー2 スイッチ2-1 スイッチ2-2
OFF OFF OFF ON OFF ON
OFF OFF OFF ON ON OFF
OFF OFF ON ON OFF ON
OFF OFF ON ON ON OFF
OFF ON OFF ON OFF ON
OFF ON OFF ON ON OFF
OFF ON ON ON OFF ON
OFF ON ON ON ON OFF
ON OFF ON OFF OFF OFF
ON OFF ON OFF OFF ON
ON OFF ON OFF ON OFF
ON OFF ON OFF ON ON
ON ON OFF OFF OFF OFF
ON ON OFF OFF OFF ON
ON ON OFF OFF ON OFF
ON ON OFF OFF ON ON

同様に、m = 3, n = 2 のときは72通りがあります。

標準入力から m, n がスペース区切りで与えられたとき、上記のような状態が何通りあるか求め、そのパターン数を標準出力に出力してください。
なお、m, n はともに20以下の正の整数とします。

【入出力サンプル】
標準入力
2 1

標準出力
16

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

def combin(m,n)
	ret = 1

	m.downto(n+1){|i| ret *= i}
	(m-n).downto(2){|i| ret /= i}

	return ret
end

def solve(m,n)
	b_on = combin(m,n)

	p_on = combin(2*n,n)
	p_off = 2**(2*(m-n))

	return b_on * p_on * p_off
end

# main
while line = gets
	line.strip!
	next if line.empty?

	m,n = line.split.map{|a| a.to_i}
	p solve(m,n)
end

解説

プログラムと言うより数学の問題と思います。

考え方

まず、ブレーカーについて考えます。
ブレーカーがOFFになっている場所はスイッチをONにしようがOFFにしようが電球は点灯しません。なのでスイッチの反転で点灯している電球の数が変わるのはONになっているブレーカーの場所だけです。

1つのブレーカーに繋がっている電球は2個なので、スイッチを反転して点灯している電球の数が同じと言うことは、n個のONのブレーカーに対してn個の電球が点灯していると言うことになります。
つまり、点灯している電球の数とONのブレーカーの数は同じでなければなりません。

m個のブレーカーのうちn個がONの組み合わせはmCnです。
更に、ブレーカー毎に2個の電球があるので最初に点灯している電球の組み合わせは2nCnです。
そして、ブレーカーがOFFの電球のスイッチのON/OFFのパターンは22(n-m)です。

これらの積が答えになるので、mCn * 2nCn * 22(n-m)を求めれば良いわけです、

main

入力値を数値にしてm, nをsolve()に渡し、結果を印字します。

solve(m,n)

考え方の通り、mCn * 2nCn * 22(n-m)を求めます。

combin(m,n)

mCnを求めます。

雑感

この問題はプログラムでパターンを数えることをせず、最初から考え方に書いた通りの数学の問題として解きました。と言うよりも、問題の操作を愚直にプログラムで実装するより数式を考えた方が容易でした。