CodeIQ：タワー・ビルディング

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「タワー・ビルディング」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
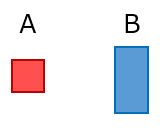
A を一辺が 1 の立方体のブロックとし、B を縦が 1、横が 1、高さが 2 の直方体のブロックとします。
（下は横から見た図です。）

fig.1

自然数 n, a, b に対し、A を最大 a 個、B を最大 b 個使って、縦が 1、横が 1、高さが n の直方体の塔を作ります。
このときの積み上げ方の場合の数を F(n, a, b) と定義します。

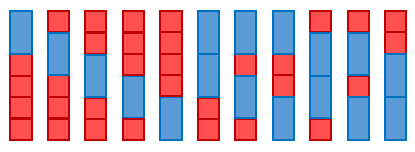
例えば F(6, 4, 2)＝11 です。以下に示します。
fig.2

同様に、F(4, 3, 1)＝3, F(4, 4, 4)＝5, F(5, 2, 1)＝0, F(10, 5, 3)＝35 です。
また、F(100, 50, 50) を 1000003 で割った余りは 765461 となることが確かめられます。

標準入力から、自然数 n, a, b（1 ≦ n ≦ 500, 0 ≦ a ≦ n, 0 ≦ b ≦ n）が半角空白区切りで与えられます。
標準出力に F(n, a, b) を 1000003 で割った余りを出力するプログラムを書いてください。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

def solve(n, a, b)
	s = [n, a, b].join(',')
	return $Memo[s] if $Memo[s] != nil
	return 0 if (a < 0) || (b < 0)
	return 1 if n == 0

	ret = 0
	ret += solve(n-1, a-1, b)
	ret += solve(n-2, a, b-1)
	ret %= 1000003

	$Memo[s] = ret
	return ret
end

# main
while line = gets
	line.strip!
	next if line.empty?

	n, a, b = line.split.map{|v| v.to_i}
	p solve(n, a, b)
end

解説

この出題者の問題としては珍しく、普通にメモ化再起の問題でした。
なのでOEISのお世話になっていません。

考え方

基本的には再起でできます。
つまりaかbを1個減らし、減らしたのがaならn-1、bならn-2としてもう一度同じ操作をするわけです。
それでa≧0かつb≧0でn=0なら1パターン見つけたのとになるので1を返し。a<0かb<0ならNGなので0を返します。

答えは1000003で割った余りなので再帰呼び出しの結果を1000003で割った余りを足し合わせれば答えになります（modの性質です）。

あとは引数をキー、その引数の時の結果を値にしたメモを作成すればOKです。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(n, a, b)

考え方の通りに実装します。

まず、$Memoに答えがあればそのパターンは計算済みなのでそれを返します。
a<0かb<0の時はNGなので0を返します。
そうでなくて、n=0ならOKなので1を返します。

それ以外の場合はaかbを1減らし、aを減らした時はn-1、bを減らした時はn-2を引数としてsolve()を再帰呼び出しします。
retを加算し、1000003で割った余りをretとします。

最終的に戻ってきた時のretが答えになります。

雑感

この出題者の問題としては珍しく、単純なメモ化再起でできました。
本当は漸化式にできるのかもしれませんが私にはわかりません。