プログラム解説：CodeIQ「ツリーの中にない数」

問題の概要

問題を引用します。

【概要】
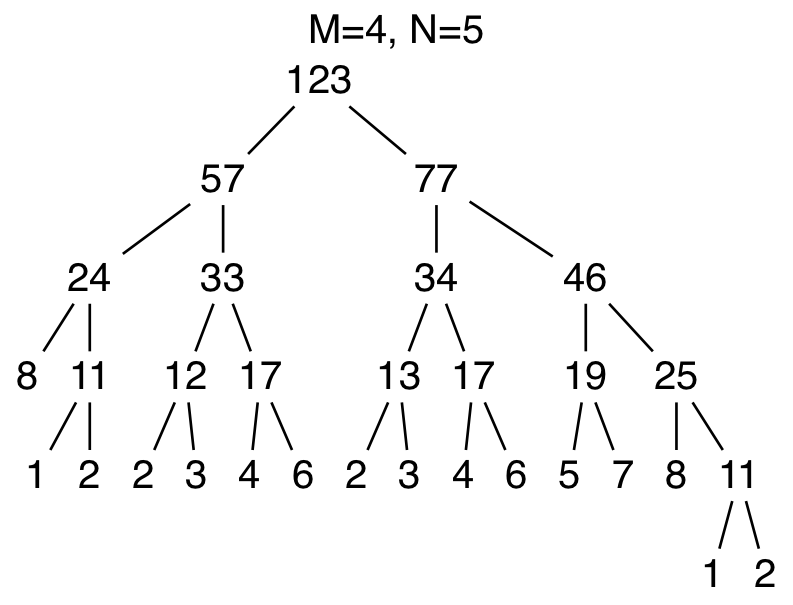
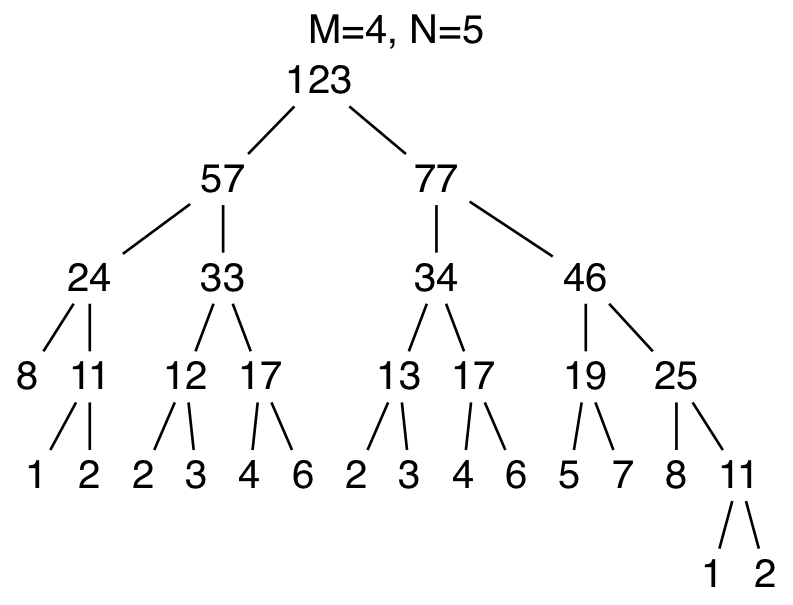
数が並んでいるツリーがあります（右図）。

だいたいどの要素にも子供が2つあります。
2つの子供は
親×(二分の一)-M( 端数切り捨て。M は入力で指定 )
親×(三分の二)-N( 端数切り捨て。N は入力で指定 )
です。
ただし、子の値が正の整数にならない場合はその子要素は存在しないことにします。

ルートの要素と M と N を指定します。
ツリーに現れない正の整数で、もっとも小さな値を計算してください。

【入出力】
入力は
のようになっています。
ルート要素、M、N が空白区切りで並んでいます。

出力は、普通に10進数です。
図の通り、ツリーに現れない最小の正の整数は 9 なので
9
を出力すれば正解です。

【例】

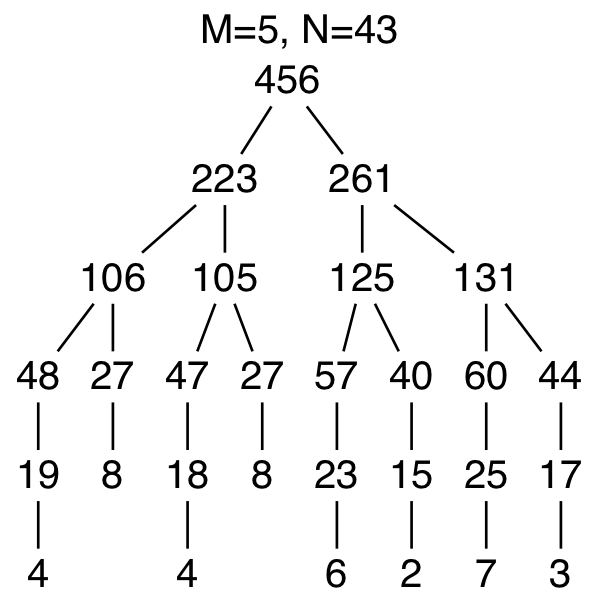
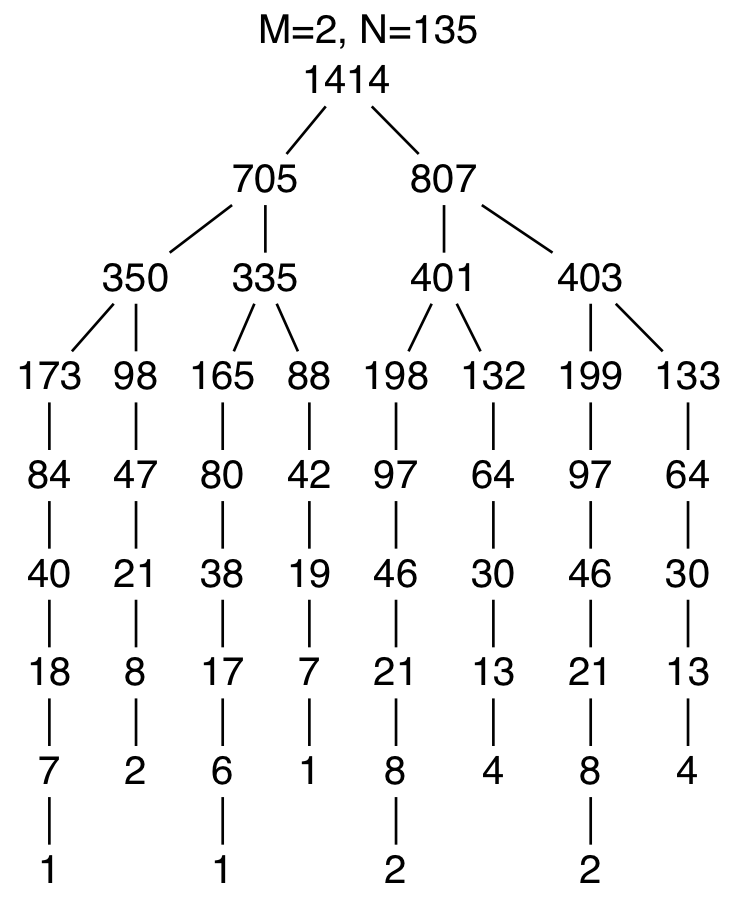
入力出力ツリー

123 4 5 9

456 5 43 1

414 2 135 3

【補足】
不正な入力に対処する必要はありません。
0 < ルート要素 ≦ 二十億です。
0 ≦ M ≦ 千, 0 ≦ N ≦ 千です。
ルート要素、M、N はいずれも整数です。

入力	出力	ツリー
123 4 5	9
456 5 43	1
414 2 135	3

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Nums = {}

def makeNums(r, m, n)
	return if $Nums[r]
	return if r <= 0

	$Nums[r] = true

	makeNums(r/2 - m, m, n)
	makeNums(2*r/3 - n, m, n)
end

def search()
	nums = $Nums.keys.sort

	x = 0
	for n in nums
		break if n != x+1
		x = n
	end

	return x+1
end

def solve(r, m, n)
	makeNums(r, m, n)
	return search()
end

# main
while line = gets
	line.strip!
	next if line.empty?

	r, m, n = line.split.map{|a| a.to_i}
	p solve(r, m, n)
end

解説

ツリーは辿りませんでした。

考え方

私のコードは単純で、ツリーに出現する数を全て求め、その中で出現しない最小の数を線形に探しています。

ツリーに出現する数は問題の通りに計算し、連想配列に{値=>true}の形で保持します。
この時、すでに出現した数があった場合、それ以降の計算は必要がない（同じ数しか出現しない）ので計算を打ち切ります。

計算が終わったら連想配列のキーの配列を取得してソートし、1から順に添字番号+1と一致しない数になったところでその値を返せば答えになります。

main

入力値を数値にし、それぞれをsolve()に渡し、結果を印字します。
$Numsはツリーに出現する数を記録する連想配列です。

solve(r, m, n)

makeNums()でツリーに登場する数を全て求めます。
search()で出現しない最小の数を探して返します。

makeNums(r, m, n)

問題の通りにツリーの子の数を再帰で計算します。
引数rは子を計算する元になる数、mとnは入力値のMとNです。

rが$Numsにある場合、それ以下の子は同じ数しか出現しないので計算をやめます。
rが0以下は計算する必要がないのでやめます。

あとは左右の子の値を計算してmakeNums()を再帰呼び出しします。

search()

ツリーに出現しない最小の数を求めます。
$Numsのキーをソートすると[1,2,3,...]となります。
この時、添字番号+1とその場所の値が異なる場合、そこで値が跳んでいるので、その添字番号+1が出現しない最小数になります。

単純に線形探索します。

雑感

問題を解いたらもらえるバッジに「ツリーをたどる問題はこれでばっちりかもしれません。」とありましたが、ツリーを辿っていないのでバッチリではないと思います。

CodeIQ：ツリーの中にない数