CodeIQ：ストレート・ラインズ

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「ストレート・ラインズ」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
2 以上の自然数 n に対し、n×n の格子状に並んだ点を考えます。
これらの点のうちちょうど 2 個の点を通る直線の数を F(n) と定義します。

例えば F(2)＝6 です。題意を満たす直線は以下の 6 通りです。
fig.1

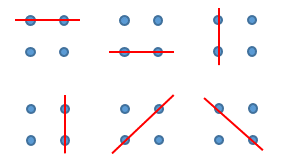
また、F(3)＝12 です。題意を満たす直線は以下の 12 通りです。
fig.2

同様に、F(4)＝48, F(5)＝108, F(6)＝248, F(7)＝428, F(10)＝1900 となることが確かめられます。

標準入力から、自然数 n （2 ≦ n ≦ 40）が与えられます。
標準出力に F(n) の値を出力するプログラムを書いてください。

私のプログラム

Rubyで解答しています。

def f(n,k)
	ret = 0

	for x in -n..n
		next if (k*x).abs >= n
		for y in -n..n
			next if (k*y).abs >= n

			# fomulaの(x,y)=1は最大公約数が1のことらしい
			next if x.gcd(y) != 1
			ret += (n-(k*x).abs)*(n-(k*y).abs)
		end
	end

	return ret
end

def a018809(n)
	return (f(n,3) - 2*f(n,2) + f(n,1)) / 2
end

# main
while line = gets
	line.strip!
	next if line.empty?
	p a018809(line.to_i)
end

解説

★★★の問題です。
OEIS直行でした。

考え方

OEIS直行なので考え方は説明できません。
問題に示された数列が長かったのでOEISでは容易に検索できました。
A018809がその答えです。

main

入力値を数値にしてa018809()に渡し、結果を印字します。

a018809(n)

問題を解きます。
OEISで見つけたfomulaの通りです。

f(n,k)

A018809のfomulaにあったf(n,k)を実装しただけです。

雑感

OEIS直行ですぐに見つけたのはよかったのですが、fomulaが読めない（苦笑）。
コードのコメントにもありますがfomulaにあった(x,y)=1がなんのことか分からない。関連のリンクか何かを見ていたらgcdという単語が出てきたので、調べたら最大公約数とあったので、x,yは互いに素かな？ と思ってやって見たら上手くいったという結果です。