CodeIQ:棒の長さを最小にするモビール
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「棒の長さを最小にするモビール」(CodeIQ)を参照してください。
問題の概要
おしゃれなインテリアとして「モビール」があります。
Wikipedia:モビール
ここでは、同じ大きさの n 個の飾りを、糸と棒を使ってバランスを取ることを考えます。
ただし、棒の長さは整数で表され、棒の長さを整数で分割した位置にしか糸を吊るせないものとします。
一般的には一つの棒の途中など複数箇所で飾りを吊るしますが、ここでは簡単にするため「棒の両端にのみ」飾りを吊るすことにします。
また、バランスを取るときに糸や棒の重さは考えなくてよいものとします。
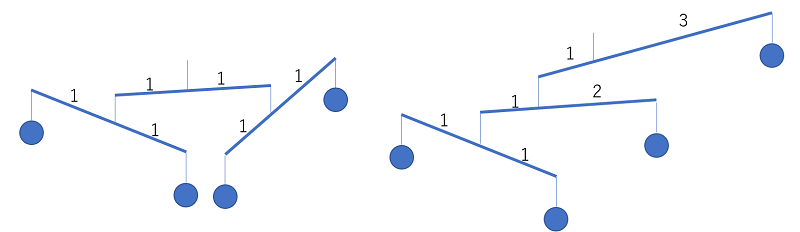
例えば、n = 4 のとき、以下のような吊るし方が考えられます。
このとき、左の図では棒の長さの合計が6なのに対し、右の図では9となっています。
そこで、棒の長さの合計が最小になるような吊るし方を考えます。
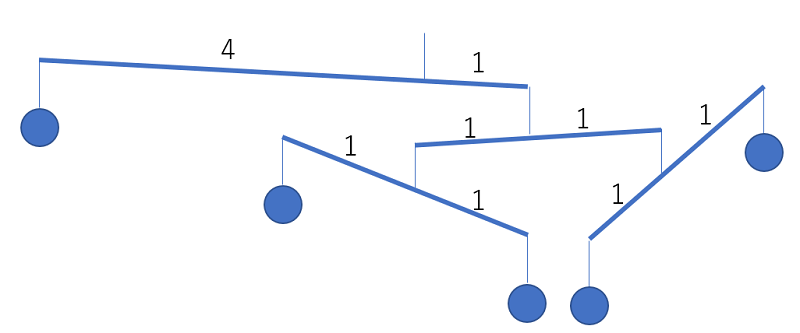
例えば、n = 5 のときは、以下のような吊るし方をすると棒の長さの合計が11で最小になります。
標準入力から n が与えられたとき、棒の長さの合計が最小になるような吊るし方を求め、その棒の長さの合計を標準出力に出力してください。
なお、n は最大でも500以下の正の整数とします。
【入出力サンプル】
標準入力
4
標準出力
6
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
$Memo = {}
def solve(n)
return $Memo[n] if $Memo[n] != nil
return 0 if n <= 1
ret = 0xfffffffffffffff
for i in 1..(n/2)
j = n-i
a = solve(i)
b = solve(j)
r = Rational(i, j)
s = r.numerator + r.denominator + a + b
ret = s if s < ret
end
$Memo[n] = ret
return ret
end
# main
while line = gets
line.strip!
next if line.empty?
p solve(line.to_i)
end
解説
考え方
1本の棒の両端にしか次の棒か重りは吊るされないので、入力値(重りの数)を左右に割り振ってゆけば良いわけです。重りの重さが同じなので、重り合計が反対側の棒の長さの比率と同じになります。
例の上の図の左の図を見てください。一番上の棒は1:3になっており、重りの数は3:1になっています。
つまり、入力値nに対しi=1..n/2とj=n-iに分けるという操作を再帰的に行い、その合計が最小になるようにすれば良いわけです。半分以上の長さになると左右反転しただけなので考慮する必要はありません。
ただし、比率が2:6のようになる場合は1:3のように公約数で割る必要があります(RubyにはRationalがあるので簡単です)。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n)
考え方の通りに実装します。
メモ化のことは置いておきます。
まず、終了条件は引数が1になった時で、この時はそれより下の棒の長さがないので0を返します。
retは棒の長さの合計です。
10〜20行目のループで重りを分割します。
iが左側に割り振った重りの数、jが右側の重りの数です。
それを再帰的にsolve()に渡して、得られた結果と割り振った値を合計します(17行目)。この時、公約数で割れるなら割るためi,jをRationalに渡します。これで既約分数になるので分母と分子を取り出せば公約数で割った値になります(16行目)。
合計値がretより小さければretを更新します。
最終的に得られたretが答えなので返却します。
最後にメモ化の話です。
入力値nに対して最小値はいつも同じになるのでnをキー、その時のretを値とした連想配列をメモとして作成します。入力値に対してメモがあればそれを返すことで高速化できます。
雑感
わかりやすい良い問題だな、と思いました。
メモ化再帰の例題として最適なんじゃないかな?