CodeIQ:円テーブルで席替え
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「円テーブルで席替え」(CodeIQ)を参照してください。
問題の概要
先生1人と生徒 n-1 人の、合わせて n 人が丸いテーブルに座っています。
途中で席替えをして、隣の人を変えることにしました。
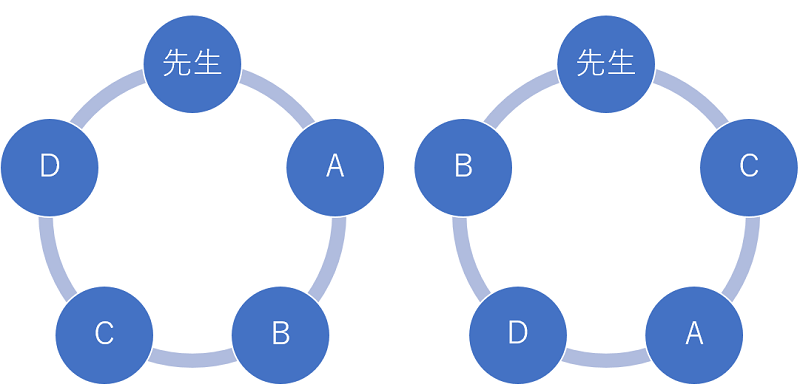
例えば、n = 5 のとき、最初に左図のように座っていると、右図のように席替えをすればすべての人の隣が変わることになります。
このとき、先生は動かないものとします。
標準入力から n が与えられたとき、席替えをして両隣の人が変わるような並び順は何通りあるかを求め、その数を標準出力に出力してください。
n = 5 のときは、上記以外に右図の左右を反転したパターンがありますので、標準出力に「2」を出力します。
なお、n は n ≦ 10を満たす正の整数とします。
【入出力サンプル】
標準入力
5
標準出力
2
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def check(arr, n)
for i in 0...n
l = ((i-1) >= 0) ? i-1 : n-1
r = ((i+1) < n) ? i+1 : 0
vl = ((arr[i]-1) >= 0) ? arr[i]-1 : n-1
vr = ((arr[i]+1) < n) ? arr[i]+1 : 0
return 0 if (arr[l] == vl) || (arr[l] == vr) || (arr[r] == vl) || (arr[r] == vr)
end
return 1
end
def solve(n)
arr = (1...n).to_a
ret = 0
arr.permutation(){|ptn|
ret += check([0] + ptn, n)
}
return ret
end
# main
while line = gets
line.strip!
next if line.empty?
p solve(line.to_i)
end
解説
考え方
これを配列で表現すると初期状態は[0,1,2,…,n-1]と並んでいるわけです。円になっているので最後の要素は最初の要素と隣り合っているとみなします。
すると、並び替え後はある数の左右にある値が、その数±1でなければ良いわけです。
そして、先生は固定なので実際は(1..n-1)の順列が並び順の全パターンで、これは362880通りしかないため全部列挙してチェックしても時間的に間に合います。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n, r, ptn, now)
1〜n-1の値の配列の順列を列挙し、check()でチェックします。この時、0(先生)は固定なので最初の要素として、生成した並び順の先頭に追加します。
check()は正しい並び順なら1、違うなら0を返すので結果を加算して返却すれば答えになります。
check(arr, n)
並び順が正しいかをチェックします。
arrは並び順の配列、nは要素数です。
4行目からのループのiは配列の要素番号です。
l,rは現在チェックしている要素番号の左右の要素番号で、配列の先頭の左は末尾、末尾の右は先頭になるようにしています(5〜6行目)。
vl,vrは現在チェックしている値の並び替え前の値です。これも0より小さくなった場合はn-1、nになった場合は0にしています(8〜9行目)。
後は現在の値の左右の要素(arr[l]とarr[r])がそれぞれ元の値(vlとvr)と同じだったらダメなので、その場合は0を返却して終わります(11行目)。
ループ終了までチェックを通ったらOKなので1を返却します。
雑感
多分、再起を使ってOKなパターンを組み立てた方が早いと思いますが、計算量を見積もったら余裕っぽかったのでpermitation()を使って総当たりしてしまいました。