CodeIQ：トーナメントでの想定対戦数は？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「トーナメントでの想定対戦数は？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

いよいよ夏の甲子園が始まります。
このような大会で用いられるのがトーナメント表です。
勝ち進んだことを想定し、どの投手をどの試合で使うのか検討することは珍しくありません。

今回はトーナメントにおける各チームの想定対戦数に注目します。
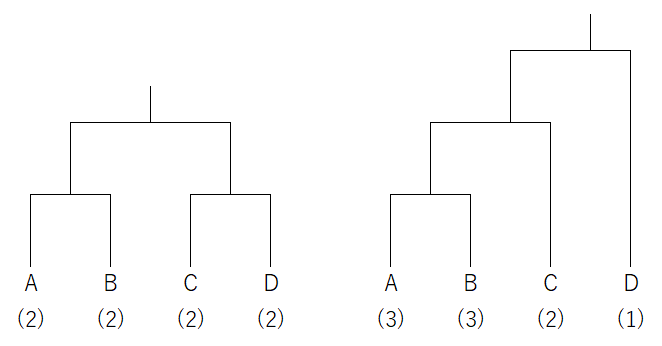
例えば、4チームでトーナメントを行うとき、トーナメント表の形として、以下のような形が考えられます。
このとき、各チームが決勝戦まで勝ち進んだときの対戦数は、それぞれ図の括弧内に書いた数字のようになります。

この想定対戦数の合計を考えると、左側の形は8、右側の形は9になります。
同様に、n チームでトーナメントを行うとき、この合計が最小になる形と最大になるような、トーナメント表の形を求めることにします。

標準入力から n が与えられたとき、考えられるトーナメント表の形について、想定対戦数の合計の「最小値」と「最大値」を標準出力にスペース区切りで出力してください。
なお、n は500以下の正の整数とします。
例えば、 n = 4 のとき、最小値は8、最大値は9ですので、以下のように出力します。

【入出力サンプル】
標準入力

4

標準出力

8 9

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

def getMax(n)
	return (n-1) + n*(n-1)/2
end

def getMin(n)
	q = n
	a = 0
	loop{
		q = q / 2
		break if q == 0
		a += 1
	}

	b = n - 2**a
	c = (n-2*b)

	return c*a + 2*b*(a+1)
end

# main
while line = gets
	line.strip!
	next if line.empty?

	mx = getMax(line.to_i)
	mn = getMin(line.to_i)

	printf("%d %d\n", mn, mx)
end

解説

問題は解けていますが数学的に証明できません。

考え方

全パターン作ってみれば最大と最小を求められますが、全パターンを作る方法では時間切れが確実です。
なので最大と最小だけを計算で求めることにしました。

これは証明できていませんが、最小になるのは可能な限り均等にした場合（問題の図の左側）、最大になるのは可能な限り偏らせた場合（問題の図の右側）のトーナメントにしたときの様です。
なのでこれを計算で求めます。

最大の方は簡単です。
図のAの位置の対戦数は(n-1)で、B〜は(n-1)、(n-2)、…、1回の対戦になります。これの合計なので(n-1)+n*(n-1)/2が答えです。

最小の方はまず図の様に完全に均等に割振れる場合、各チームの対戦数はlog₂n回です。n=5の様に余りが出る場合はこれを基本に余りの分を考慮します。
a = log₂nとします。
余りのチーム数bはb=n-2^aです。
余りのチームには対戦相手が要るので2bのチームはa+1回対戦することになります。
ということはa回対戦するチーム数cはc=n-2bです。
なので答えはc*a+2b(a+1)になります。

main

入力値を数値にしてgetMax()、getMin()に渡し、結果を得ます。
それぞれの結果を印字します。

getMax(n)

考え方の通りに結果を計算します。

getMin(n)

考え方の通りに結果を計算します。
log₂nを計算してもよかったのですが浮動小数点が嫌だったのでループで計算しました。対数時間なので大したことにはなりません。

雑感

直感的に最大、最小のトーナメント表の形はわかりますが、どうやって証明すればいいんでしょう？