CodeIQ：〇×ゲームの手順は何通り？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「〇×ゲームの手順は何通り？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
3×3のマス目を使って〇×ゲーム（三目並べ）を行います。
2人が交互に〇と×を空いているマスに記入していき、同じ記号が縦、横、斜めのいずれかに3つ並ぶとその記号の人が勝ちです。
すべてのマスが埋まっても3つ並ばないとき、その勝負は引き分けとなります。

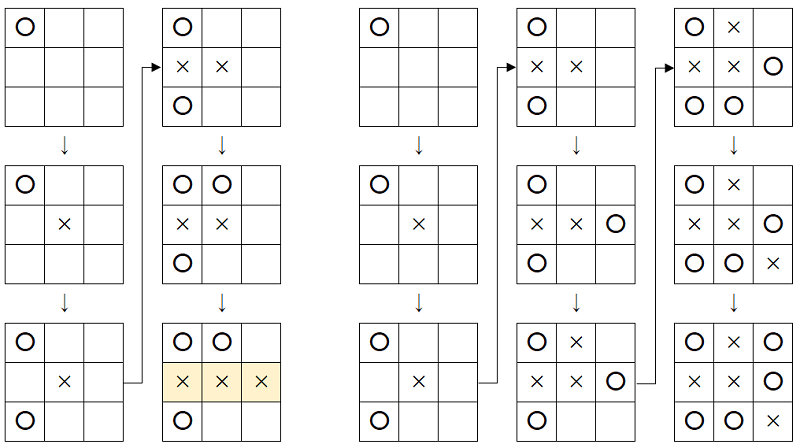
例えば、以下の左図のような順に書いていったとき、×が横に3つ並んだので×の勝ちとなります。
一方、右図のような順に書いていったとき、いずれも3つ並ばないため、引き分けとなります。
（必ず〇の人から始め、勝負が決まった時点で終了するものとします）

fig.1

標準入力から整数 n が与えられたとき、ちょうど n 手でどちらか一方が勝つまでの手順が何通りあるかを求めてください。
なお、n は5以上9以下の整数です。

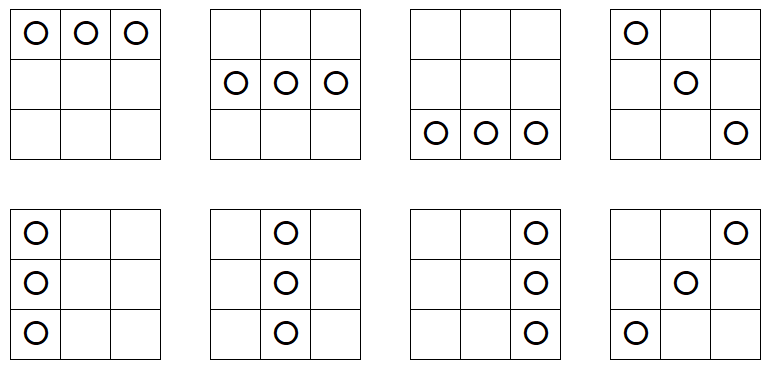
例えば、n = 5 のとき、〇の配置は、以下の8通りが考えられます。
それぞれについて、残りのマスのうち2箇所に×が入るため、手順を考えると全部で1440通りあります。
fig.2

【入出力サンプル】
標準入力
5

標準出力
1440

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

def check(brd, pl)
	return true if (brd[0]==pl) && (brd[1]==pl) && (brd[2]==pl)
	return true if (brd[3]==pl) && (brd[4]==pl) && (brd[5]==pl)
	return true if (brd[6]==pl) && (brd[7]==pl) && (brd[8]==pl)
	return true if (brd[0]==pl) && (brd[3]==pl) && (brd[6]==pl)
	return true if (brd[1]==pl) && (brd[4]==pl) && (brd[7]==pl)
	return true if (brd[2]==pl) && (brd[5]==pl) && (brd[8]==pl)
	return true if (brd[0]==pl) && (brd[4]==pl) && (brd[8]==pl)
	return true if (brd[2]==pl) && (brd[4]==pl) && (brd[6]==pl)
	return false
end

def solve(n, i, brd)
	return $Memo[brd] if $Memo[brd] != nil
	chk = check(brd, i%2)

	if (i==n) && chk then return 1
	elsif (i==n) && !chk then return 0
	elsif (i!=n) && chk then return 0
	end

	ret = 0
	i += 1

	for k in 0...9
		next if brd[k] != nil
		nb = brd.dup
		nb[k] = i%2

		ret += solve(n, i, nb)
	end

	$Memo[brd] = ret
	return ret
end

# main
while line = gets
	line.strip!
	next if line.empty?

	p solve(line.to_i, 0, Array.new(9))
end

解説

これはOEISにあるだろうと思って調べたら、結果はありましたが式がなかったので自力で考えました。でも、普通にメモ化再帰でできます。

考え方

素直に再帰で三目並べを実装し、メモ化すればできます。

三目並べのパターンを列挙するのは次の様にします。
まず、要素数9の配列を用意し○も×も書かれていない場所をnil、○を1、×を0として扱うこととします。盤面を素直に実装すると二次元配列ですが、コピーが面倒なので一次元配列で0〜2を1行目、3〜5を2行目、6〜8を3行目として扱います。

関数は入力値と現在何手目かと盤面を引数にとります。
盤面をチェックし、手番が入力値と同じ回数でその手番のプレイヤーが勝っていたら1を返します。手番が入力値と同じでどちらも勝っていないか手番が入力値と異なるのにどちらかが勝っていたら0を返します。
それ以外の場合は次の手番の手を打ちます。手番が偶数なら0、奇数なら1を盤面のnilの場所のどこかに書き込みます。

最終的に戻り値を合計すれば答えになります。

メモは盤面をキーにしてその盤面のパターン数を値とすればOKです。

main

入力値を数値にしてsolve()の第一引数、第二引数は手番で初期値0、第三引数は盤面で全要素がnilの要素数9の配列を渡し、結果を印字します。

solve(n, i, brd)

三目並べのパターンを列挙します。

18行目はメモに計算結果があるかをチェックし、あればその値を返します。
19行目でどちらかが勝っているかをチェックします。奇数手番の場合は1、偶数手番の場合は0がプレーヤーなので、手番iを2で割った余りを勝ち負け判定対象のプレイヤーとします。
21行目は手番が入力値の時にその手番のプレイヤーが勝っている場合で1を返します。
22行目は手番が入力値の時に勝ちが確定していない場合です。この場合は問題のパターンにならないので0を返します。
23行目は手番が入力値でない時にどちらかが勝っている場合で、これも問題のパターンにならないので0を返します。

27行目で手番を1つ進めます。
29行目のループで盤面の空いている場所（nilの要素）に手番の値（手番iを2で割った余り）を書き込み、solve()を再帰呼び出しします。
返却値を全て加算することでパターン数を集計します。

37行目で特定の盤面から条件を満たす結果のパターン数をメモに記録します。
retを返却して終了します。

check(brd, pl)

手番プレーヤーが勝っていればtrue、そうでなければfalseを返します。
単純に、手番プレイヤーの値（引数pl）が盤面（引数brd）の縦横斜めに並んでいるかを全てチェックします。

雑感

最初に書いた様にOEISでtic-tac-toeを調べると答えが見つかるのですが、式がなかったので自分で実装しました。盤面を配列にしましたが、2bitずつ使って0b01と0b10を手番プレイヤーの値、0b00を空きとして扱えばもう少し簡潔かつ高速に実装できました。