CodeIQ：キャンディ・アンド・チョコレート

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「キャンディ・アンド・チョコレート」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

n 個のキャンディをグループに分けます。
グループの最大のキャンディの個数が k 個となるような分け方の数を F(n, k) と定義します。

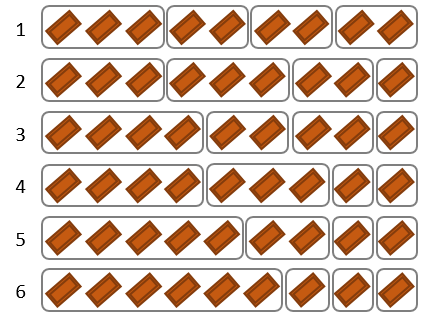
例えば、F(8, 3)＝5 です。このときの分け方を以下に示します。
なお個々のキャンディを区別せずに扱う点に注意してください。

,br>
同様に、F(4, 2)＝2，F(20, 6)＝90 となることが確かめられます。

次に、n 個のチョコレートをグループに分けます。
グループの数がちょうど k 個となるような分け方の数を G(n, k) と定義します。
例えば、G(9, 4)＝6 です。このときの分け方を以下に示します。

同様に、G(4, 2)＝2，G(18, 4)＝47 となることが確かめられます。

標準入力から、自然数 n と k （1 ≦ k ≦ n ≦ 100）が半角空白区切りで与えられます。
標準出力に F(n, k)＋G(n, k) の値を出力するプログラムを書いてください。

例えば入力が「4 2」の場合は、F(4, 2)＋G(4, 2) の値である「4」を出力してください。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

def partition(n, k)
	return $Memo[[n,k]] if $Memo[[n,k]] != nil
	return 1 if (n == 1) || (k == 1)
	return 0 if (n < 0) || (k < 0)

	ret = partition(n-k, k) + partition(n, k-1)
	$Memo[[n,k]] = ret
	return ret
end

def solve(n, k)
	return 2 * (partition(n,k) - partition(n, k-1))
end

# main
while line = gets
	line.strip!
	next if line.empty?

	n,k = line.split.map{|v| v.to_i}
	p solve(n,k)
end

解説

★★★の問題ですが、この出題者の問題で★★★としてはやや簡単かと思います。
ただし、分割数の問題と気づけば、ですが。

考え方

最初に書いた通り、これは分割数の問題です。
キャンディは「自然数nを最大値をkとする数で分割した場合の分割数」、チョコレートは「自然数nをちょうどk個の数に分割した場合の分割数」のパターン数です。

ここで最大のポイントは「自然数nを最大値をkとする数で分割した場合の分割数」と「自然数nをちょうどk個の数に分割した場合の分割数」は等しいことです。なのでどちらかを求めて結果を2倍すれば答えになります。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

partition(n,k)

nをk以下の数で分割した場合のパターン数を求めます。
分割数のパターン数を求める方法は検索すると色々見つかります。私はこのサイトを参考にしました。
メモ化して高速化しています。

注意点は「nをk以下の数で分割した場合のパターン数を求める」関数だということです。n=8,k=3だと最大の数が2や1の場合も結果に含まれるので注意が必要です。

solve(n,k)

自然数nを最大値をkとする数で分割した場合の分割数」を求めその結果を2倍して返します。partition()は「nをk以下の数で分割した場合のパターン数を求める」のでpartiton(n,k)-partition(n,k-1)として「自然数nを最大値をkとする数で分割した場合の分割数」を求めています。
結構な無駄ですがnの最大が100くらいならpartition()が十分高速なので大丈夫です。

雑感

問題を読んで分割数の問題ということにはすぐに気づきましたし、「自然数nを最大値をkとする数で分割した場合の分割数」と「自然数nをちょうどk個の数に分割した場合の分割数」は等しいこともおぼろげに覚えていたので（確認のために調べ直しましたが）割とすぐにできました。
ただ、分割数の問題はいくつかやっていますが、いつも結構面倒臭いです。何か毎回違うアルゴリズムで実装しているきもするし。