CodeIQ：上下左右に箱を並べよう

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「上下左右に箱を並べよう」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
大手衣料品店のスマートフォンアプリとコラボレーションして話題になっている、ゲーム機での人気ゲームがあります。
(例えばこのようなゲームがイメージです→) http://www.uniqlo.com/jp/hacoboy/　※CodeIQ外のサイトに飛びます。
このゲームのように、箱を並べるパターンが何通りあるかを求めることを考えます。

ここでは図のような格子状のマスにおいて、ある位置からスタートして、上下左右の隣り合う位置に箱を配置していきます。
すでに箱が配置されている位置、開始位置には箱を配置できません。
なお、上記のゲームでは最初に下方向に配置することはできませんが、本問では最初から下方向も可能とします。

配置する箱の数 n が与えられたとき、その箱の配置方法が何通りあるかを求めます。
ただし、できあがった位置と形だけで判断するものとし、その手順が異なっても同じ位置・同じ形であれば同じものとします。
例えば n = 3 のとき、以下のパターンはいずれも同じものとします。
fig.1

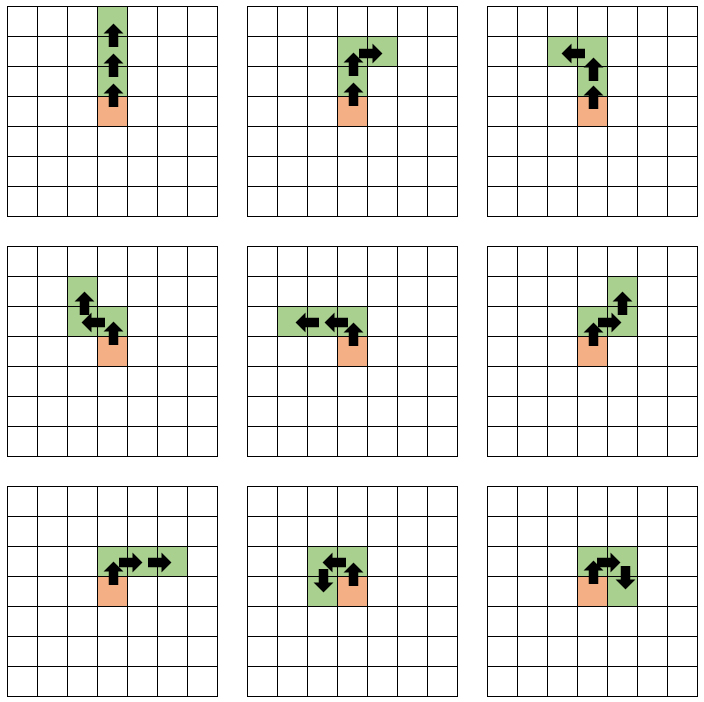
n = 3 のとき、その箱の配置方法は以下の図のように上方向からスタートするものが9通り、そのほか全部で32通りがあります。
fig.2

標準入力から n が与えられたとき、その箱の配置方法が何通りあるかを求め、標準出力に出力してください。
なお、n は 9以下の正の整数とします。

【入出力サンプル】
標準入力
3

標準出力
32

私のプログラム

Rubyで解答しています。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#!/usr/bin/ruby
 
ROT_90 = [[0, -1], [1, 0]]
ROT_180 = [[-1, 0], [0,-1]]
ROT_270 = [[0, 1], [-1, 0]]
 
def rotate(fig, to)
    ret = []
 
    for f in fig
        ret << [
            to[0][0] * f[0] + to[0][1] * f[1],
            to[1][0] * f[0] + to[1][1] * f[1]
        ]
    end
 
    return ret.sort_by{|x| [x[0], x[1]]}
end
 
def rotateAll(arr, to)
    ret = []
    for a in arr
        ret << rotate(a, to)
    end
    return ret
end
 
def make(n, st)
    dir = [[0,1], [1,0], [0,-1], [-1,0]]    # 上右下左
    queue = [st]
 
    for _ in 0...n
        nq = []
 
        while !queue.empty?
            now = queue.shift
 
            for d in dir
                nxt = [now.last[0]+d[0], now.last[1]+d[1]]
                next if now.include?(nxt)
                nq << now + [nxt]
            end
        end
 
        queue = nq
    end
 
    ret = []
    for q in queue
        ret << q.sort_by{|x| [x[0], x[1]]}
    end
 
    return ret
end
 
def solve(n)
    up = make(n-1, [[0,0], [0,1]])
    left = rotateAll(up, ROT_90)
    down = rotateAll(up, ROT_180)
    right = rotateAll(up, ROT_270)
 
    ret = up + left + down + right
    ret = ret.uniq
 
    return ret.size
end
 
# main
while line = gets
    line.strip!
    p solve(line.to_i)
end

解説

★★★の問題としてはやや簡単な気がします。
少し問題を補足しておきます。
                 
                 
  12    32   21  
  03    01   30  
                 
                 

上図の赤と青は同じですが、赤と青、緑と青は別の図形です。
問題をきちんと読めば位置も同じでなければならないことは書いてあるのですが、ちょっと迷ったので補足しておきます。

考え方

この問題で図形を作るのは容易です。
問題は同じ図形のチェックで、これを効率よくやる方法をどうするかです。

まず、オーダーを見積もってみます。
四方向に箱を置けるのでO(4n)なので、問題より最大でパターン数は262144です。それほどの数ではありませんが、同じ形のチェックを考えると計算量を減らしたいところです。

この方法で作れる図形は最初の方向を一方向に限定して作成し、それを90度、180度、270度回転しても全パターン列挙できます。最初の方向を一方向に固定するとn回がn-1回になるのでかなり計算量を減らせます。

次に同型のチェックですが私はRubyのArray#uniq()で同じものを省くことができるようにしました。RubyのライブラリがCかC++で書かれていて速いことを期待してです。
そのために、図形は座標だけを保持し、図形の座標が決定したらソートしてArray#uniq()で重複を削除することにしました。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(n)

まず、最初の箱を上方向におくパターンだけで図形を列挙します。
それを元に90度、180度、270度回転した図形の座標リストを作成します。
これらの結果得られる座標は全てソート済みです。

この座標リストを連結してArray#uniq()で重複を削除し、リストのサイズを返します。

make(n,st)

nは手順回数（入力値-1）、stは1手順目を配置した座標リストで実際には[[0,0], [0,1]]が渡ってきます。

dirは箱を置く方向のリストです。
queueには途中状態の図形のリストが入ります。初期状態は引数stだけが入っています。

手順回数（入力値-1）だけループし、queueから最初の要素を取り出して、dirの各方向に箱を配置します。
この時、すでに箱が置かれている場所に再度置こうとした場合は不正な操作なので無視します。
箱が置けた場合、次の候補（変数nq）にその座標リストを追加します。
queueが空になったらnqでqueueを置換します。
n（入力値-1）回の操作を終えたら作成可能な図形が列挙されているので、x座標（優先）、y座標（2番目のソート条件）でソートします。これで同じ図形は同じ座標が同じ順番で並んでいます。

ソート済みの座標リストを返却します。

rotate(fig, to)

図形の回転を計算します。高校で習うベクトルの回転です。
figは図形1つ分の座標リストで、toは回転のための行列です。toには定数ROT_A、ROT_B、ROT_Cのいずれかを受け取ります。
回転後の座標リスト（ソート済み）を返却します。

rotate(arr, to)

arrは図形の座標リストの配列で、その全てに対してtoに指定した行列（定数ROT_A、ROT_B、ROT_Cのいずれか）で回転後の図形の座標リストの配列を返します。

雑感

単純に総当たりのコードです。多分、パターン数だけを計算することもできると思いますが私には数学が足りません。
この問題が★★ではなく★★★なのは座標の回転の知識が必要な分★1個増えたのでしょうか？