CodeIQ：指定された回数で移動できる経路は何通り？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「指定された回数で移動できる経路は何通り？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

横に m マス、縦に n マス並んだ格子状のマスがあり、左上の隅から右下の隅までマスの周囲または対角線に沿って移動することを考えます。
ただし、対角線は左上から右下への線のみ可能とします。
（縦でも横でも斜めでも、いずれも1回で1マス分移動します）
移動は「右」「下」「右下」のいずれかとし、左や上、左上などに移動することはできません。

標準入力から m, n と合わせて移動回数 a がスペース区切りで与えられるとき、ちょうど a 回の移動で右下の隅に到達する経路の数が何通りあるかを求め、標準出力に出力してください。
ただし、m, n は20以下の正の整数、a は m + n 以下の正の整数とします。

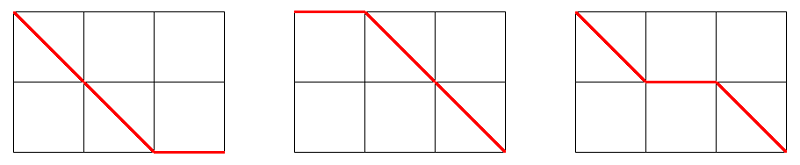
例えば、m = 3, n = 2, a = 3のとき、以下のような3通りが考えられます。

【入出力サンプル】
標準入力

3 2 3

標準出力

3

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

def solve(m, n, a, pos)
	return 0 if (pos[0] > m) || (pos[1] > n)
	return $Memo[[pos[0], pos[1], a]] if $Memo[[pos[0], pos[1], a]] != nil
	if a == 0 then
		if (pos[0] == m) && (pos[1] == n) then return 1
		else return 0
		end
	end

	dir = [[1,0], [0,1], [1,1]]
	ret = 0
	for d in dir
		ret += solve(m, n, a-1, [pos[0]+d[0], pos[1]+d[1]])
	end

	$Memo[[pos[0], pos[1], a]] = ret
	return ret
end

# main
while line = gets
	line.strip!
	next if line.empty?

	m,n,a = line.split.map{|v| v.to_i}
	p solve(m, n, a, [0,0])
end

解説

よくあるメモ化再帰の問題です。

考え方

移動は単純に再帰で実現できます。
引数に現在の座標と移動回数の残りをとる関数を用意し、右、下、右斜め下に移動し、新しい座標と移動回数の残りを1減らしたものを引数として再帰的に関数を呼び出します。
終了条件は右下に達するか移動回数残りが0になった時で、移動回数残りが0かつ右下に到達した場合だけ1を返却し、それ以外は0を返却することで実現できます。

あとはこれをメモ化すればよく、メモのキーには座標と残り移動回数、メモの値はその場所からの移動パターン数を記録しておけばOKです。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(m,n,a,pos)

引数m,n,aは入力値です。
posは現在の座標（行,列）です。

6〜12行目は終了条件のチェックです。
座標が範囲外の時はダメなので0を返します（6行目）。
メモに結果がある場合は再計算せず値を返却します（7行目）。
a（残り移動回数）が0の場合（8行目）、座標が右下なら1を返却し（9行目）、それ以外なら0を返却します（10行目）。

dirは下、右、右下への移動を示す値です。
retは引数の座標、残り移動回数から右下に到達する経路のパターン数の合計です。

16〜18行目のループで移動し、その座標と残り移動回数を1減らした値でsolve()を再帰呼び出しし、結果をretに加算します。

20行目でメモに当該引数の場合のパターン数を記録します。
retを返却します。

雑感

よくあるタイプの問題だったので簡単に終わりました。
もし、これが上、左、左上への移動が認められているならかなり苦労したと思います。