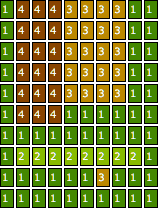CodeIQ:極めよプログラミング道!【実力判定:Sランク】その2
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「極めよプログラミング道!【実力判定:Sランク】その2」(CodeIQ)を参照してください。
問題の概要
【問題】
1辺の長さが整数nの、正方形の盤面があります(1 ≦ n ≦ 3000)。
この盤面は、1辺の長さが1の正方形で、マスが区切られています。
各マスには、盤面の厚さを示す整数mが入っています(1 ≦ m ≦ 9)。
この時、盤面上で、同じ厚さだけで構成された、最も大きな正方形の面積を求めて下さい。
ただし、この盤面は、以下のアルゴリズムで生成されます(以下はJavaScriptですが、内容は汎用的なコードです)。
// 盤面生成アルゴリズム // sz - 1辺の長さ // h - 最大の厚さ var genBoard = function(sz, h) { // 盤面初期化 var arr = []; for (var i = 0; i < sz * sz; i ++) { arr[i] = 1; } // 盤面改変 var r = 1, r0, r1, r2, r3, r4; var max = sz < 100 ? sz : 100; for (var i = 0; i < max; i ++) { r0 = r = (r % 10009) * 99991; r1 = r = (r % 10009) * 99991; r2 = r = (r % 10009) * 99991; r3 = r = (r % 10009) * 99991; r4 = r = (r % 10009) * 99991; var sqrX = r0 % sz; var sqrY = r1 % sz; var sqrW = r2 % (sz - sqrX) % 100; var sqrH = r3 % (sz - sqrY) % 100; var brdH = (r4 % h) + 1; for (var x = sqrX; x < sqrX + sqrW; x ++) { for (var y = sqrY; y < sqrY + sqrH; y ++) { arr[x + y * sz] = brdH; } } } return arr; };
【入力】
標準入力から、複数行のデータが与えられます。
1行のデータは、盤面の1辺の長さ、最大の厚さの数字が、カンマ区切りで入っています。
【出力】
全ての行に対して、盤面生成アルゴリズムで盤面を生成し、最も大きな正方形の面積を、標準出力に1行ずつ出力します。
【入出力サンプル】
Input
10,4
13,5
生成される盤面を色付けした例
Output
16
25
最大面積の一例
// 10,4 +----+ 1444|3333|11 1444|3333|11 1444|3333|11 1444|3333|11 +----+ 1444 3333 11 1444 1111 11 1111 1111 11 1222 2222 21 1111 1131 11 1111 1111 11 // 13,5 +-----+ |11111|11111111 |11111|11111111 |11111|11144111 |11111|11144111 |11111|11144111 +-----+ 11122 22144111 55522 22554111 25522 22554111 25522 22511111 25522 22333311 21111 11333311 14444 11111111 11111 11111111
私のプログラム
C++で解答しています。
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
void printBoard(int* arr, int n){
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
printf("%d", arr[i*n+j]);
}
printf("\n");
}
}
int* genBoard(int sz, int h){
// 盤面初期化
int* arr;
arr = (int*)malloc(sz*sz*sizeof(int));
for(int i=0; i<sz*sz; i++){
arr[i] = 1;
}
// 盤面改変
int r = 1;
int mx = sz < 100 ? sz : 100;
for(int i=0; i<mx; i++){
int r0 = r = (r % 10009) * 99991;
int r1 = r = (r % 10009) * 99991;
int r2 = r = (r % 10009) * 99991;
int r3 = r = (r % 10009) * 99991;
int r4 = r = (r % 10009) * 99991;
int sqrX = r0 % sz;
int sqrY = r1 % sz;
int sqrW = r2 % (sz - sqrX) % 100;
int sqrH = r3 % (sz - sqrY) % 100;
int brdH = (r4 % h) + 1;
// printf("sqrX=%d, sqrY=%d, sqrW=%d, sqrH=%d, brdH=%d\n", sqrX, sqrY, sqrW, sqrH, brdH);
for(int x=sqrX; x<(sqrX + sqrW); x++){
for(int y=sqrY; y<(sqrY + sqrH); y++){
arr[x+y*sz] = brdH;
}
}
// printBoard(arr, sz);
}
return arr;
}
int min(int a, int b, int c){
int ret = a < b ? a : b;
return ret < c ? ret : c;
}
int solve(int* brd, int sz){
int* ret;
ret = (int*)malloc(sz*sz*sizeof(int));
for(int i=0; i<sz*sz; i++){
ret[i] = 1;
}
int mx = 0;
for(int row=1; row<sz; row++){
for(int col=1; col<sz; col++){
ret[row*sz+col] = min(
brd[(row-1)*sz+col] != brd[row*sz+col] ? 0 : ret[(row-1)*sz+col],
brd[row*sz+(col-1)] != brd[row*sz+col] ? 0 : ret[row*sz+(col-1)],
brd[(row-1)*sz+(col-1)] != brd[row*sz+col] ? 0 : ret[(row-1)*sz+(col-1)]
) + 1;
if(ret[row*sz+col] > mx){mx = ret[row*sz+col];}
}
}
// printBoard(ret, sz);
free(ret);
return mx*mx;
}
int main(void){
char line[16] = {0};
int n = 0;
int m = 0;
while( fgets(line, sizeof(line), stdin) != NULL ){
sscanf(line, "%d,%d", &n, &m);
int* brd = genBoard(n,m);
int ret = solve(brd,n);
printf("%d\n", ret);
free(brd);
}
}
解説
難しいというか、スクリプト言語ではn=3000だと1秒をきれない気がします。
考え方
どうやって最大の正方形を見つけるかですが、これは動的計画法でできます。
まず、マップと同じサイズの領域を用意します。
これは、マップの同じ座標を右下とした場合にできる最大の正方形の1辺の長さを記録します。
左端の列と最上段の行にできる正方形は1(そこを右下にした場合1以上の正方形は作れない)なので、左端の列と最上段の行を1で初期化します(実際には全体を1で初期化して問題ない)。
そして、座標(1,1)から順に値を決めてゆきます。
任意の座標を右下とした時にできる正方形の最大サイズは、その座標の左、上、左上の値のうち最小のもの+1になります。ただし、今回は同じ高さという制限があるので、左、上、左上の高さが現在の座標の高さと違う場合は左、上、左上の値を0とみなします。
これを座標(1,1)から右下まで計算し、最大の値を取得すれば答えになります。
main
入力値を数値にし、genBoard()でマップを生成します。
そのマップからsolve()で最大の正方形のサイズを得、結果を印字します。
genBoard(int sz, int h)
問題文のfunctionをC++に移植しただけです。
solve(n)
retは各座標を右下とした時にできる最大の正方形の辺の長さを記録する領域です。
静的に4096バイトより大きいサイズを確保すると実行時エラーになるので(今はならないのかな?)、malloc()で動的に確保します。
行、列の座標について(1,1)から右下までループしながら、retの左、上、左上の値から最小のものを選びます。高さが違う場合は0とします。
mxは最大の正方形お辺の長さで、retが完成してから最大値を探すのは無駄なので、都度最大の値を記録します。
最終的に必要なのは正方形の面積なのでmxを二乗して返します。
min(a,b,c)
a、b、cのうち最小値を返します。
Cの標準ライブラリのmin()は2つの値の小さい方を返す関数なので作成しました。
雑感
最初、いつものようにRubyでやったのですが、n=3000だと1秒を切らないのでC++で書き直しました。
この問題は解凍後にヒントが出ますが、それを見るとこの方法が想定のアルゴリズムのようです。そうすると、スクリプト言語では到底間に合わないような気が……。制限時間が1秒ではなかったのでしょうか?
しかし、久しぶりにC++(というか、任意の場所で変数宣言したかったからC++にしただけで実際にはC言語)を書いたのですが、結構忘れていて驚きました(引数の順番などは普通に忘れるの大したことはないのですが)。
配列(メモリ)確保して初期化するのに、最初calloc()を使って一発でやればできると思ってやったら変な値になって、「なんじゃ?」となってしまいました(バイト単位でしか初期化できない。今回はint単位で1にしたかった)。あと、ループでしか初期化できないことも忘れていて、何かint幅で初期化する方法なかったかなぁと、しばらく考えました。
malloc()からmemset()とかcalloc()とか散々書いてきて忘れることはないと思ってたのに。