CodeIQ:同じ形に分割
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「同じ形に分割」(CodeIQ)を参照してください。
問題の概要
横 m マス、縦 n マスの長方形があります。これを同じ形の2つの領域に分割することを考えます。
ただし、それぞれの領域はすべて縦・横でつながっている(隣り合っている)ものとします。
つまり、同じ色の領域が複数に分かれてはいけませんし、斜めの場合は隣り合っているとはみなしません。
分割する位置はマスの区切りとし、斜めに分割したり、1つのマスを複数に分けたりすることはできません。
また、分割する線の位置を決めるものとし、色が逆のパターンは1つとカウントします。
なお、「同じ形」とは点対称のように回転させて重なる形とします。
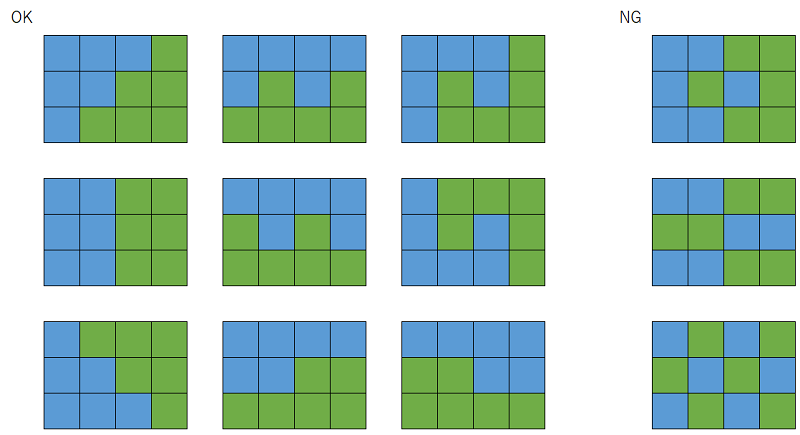
例えば、m = 4, n = 3のブロックの場合、以下の左にあるような9通りの分け方があります。
例
右のような分け方は、つながっていないためNGです。
標準入力から m と n がスペース区切りで与えられたとき、何通りの分け方があるかを求め、その数を標準出力に出力してください。
なお、m, n はともに正の整数で、 1 < m × n < 25 を満たすものとします。
【入出力サンプル】
標準入力
3 4
標準出力
9
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
class Grid
def initialize(m, n, pts, rpts)
@m = m
@n = n
@pts = pts
@rpts = rpts
end
def move()
dir = [[0,1],[1,0],[0,-1],[-1,0]] # 下右上左
rdir = [[0,-1],[-1,0],[0,1],[1,0]] # 上左下右
ret = []
for i in 0...4
np = [@pts.last[0] + dir[i][0], @pts.last[1] + dir[i][1]]
next if (np[0] < 0) || (np[1] < 0) || (@m < np[0]) || (@n < np[1])
next if @pts.include?(np)
rp = [@rpts.last[0] + rdir[i][0], @rpts.last[1] + rdir[i][1]]
nxt = Grid.new(@m, @n, @pts + [np], @rpts + [rp])
ret << nxt
end
return ret
end
def check()
if (@pts.last == @rpts.last) then return 1
elsif (@pts[-1] == @rpts[-2]) && (@rpts[-1] == @pts[-2]) then return 1
elsif (@pts.last[0] == 0) || (@pts.last[0] == @m) || (@pts.last[1] == 0) || (@pts.last[1] == @n) then return -1
elsif (@rpts.last[0] == 0) || (@rpts.last[0] == @m) || (@rpts.last[1] == 0) || (@rpts.last[1] == @n) then return -1
elsif @pts.include?(@rpts.last) && @rpts.include?(@pts.last) then return -1
else return 0
end
end
end
def count(queue)
ret = 0
while !queue.empty?
q = queue.shift
nxts = q.move()
for n in nxts
c = n.check()
if c == 1 then ret += 1
elsif c == 0 then queue << n
end
end
end
return ret
end
def solve(m,n)
return 0 if (m%2 == 1) && (n%2 == 1)
ret = 0
queue = []
for i in 1...m
queue << Grid.new(m,n,[[i,0]], [[m-i,n]])
end
ret += count(queue)
queue = []
for j in 1...n
queue << Grid.new(m,n,[[0,j]], [[m,n-j]])
end
ret += count(queue)
return ret
end
# main
while line = gets
line.strip!
next if line.empty?
m,n = line.split.map{|a| a.to_i}
p solve(m,n)
end
解説
ポイントは点対称になるということです。
考え方
ここでポイントなのが最初に書いた通り、点対称になるということです。上辺(左辺)から交点を辿るのと同時に点対称の位置にある下辺(右辺)からも上下左右反対に交点を辿ると、2分割できる場合真ん中あたりで同じ点か同じ辺にたどり着きます。2分割できない場合はたどり着いた点が反対側から辿った場合の最後の点でないか、ぶつからずに四角形の外周に到達した場合になります。
また、両側からやることで計算量を大幅に削減できます。
単純に考えて元来た場所以外の交点を辿るので計算量はO(3n)になりますが、両側からやることでnが半分になります。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(m,n)
引数m,nは入力値です。
62行目ですが、mとnの両方が奇数の場合、問題の条件通りに分割できないので0を返してしまいます。
65〜68行目は上辺、72〜75行目は左辺に開始点をとった場合の最初のスタート地点を作り処理です。
70、76行目で探索し、パターン数を加算します。
最終的にパターン数を返却します。
Grid
Gridクラスは移動経路を管理するためのクラスです。
@m、@nは問題の入力値です。
@ptsは上辺、左辺から辿った交点のリスト、@rptsはそれと対象になるように下辺、右辺から辿った交点のリストです。
Grid#move()
1回分の移動を処理します。
現在の@ptsの最後の要素からdirの各方向に移動した場合の座標を計算します(17行目)。
もし、範囲外になった(19行目)かすでに通過した点に戻った(20行目)の場合、無効な移動なので無視します。
そうでなければ@rptsの最後の要素に対して反対向きの移動を処理します(22行目、rdirはdirの反対向きの移動を表しています)。
24行目で移動後の状態を新規にGridのインスタンスとして生成し、retに追加します。
全ての移動を処理したら新たにできた状態のリストを返却します。
Grid#check()
分割が完了したか、無効な分割だったかをチェックします。
返却値が1なら分割完了、-1なら不正な分割で完了、0は分割完了ではないので継続を表します。
33行目は2方向の探索で最後の点が一緒だった場合で、2分割に成功した状態として1を返却します。
34行目は2方向の探索で最後の辺が一緒だった場合で、2分割に成功した状態として1を返却します。
35と36行目は2方向の探索が交わらず、外周に到達した場合で条件を満たしていないので-1を返します(一方の探索が外周に到達していたら、反対側の探索も外周に到達するので36行目はなくても問題ないはずです)。外周への到達をmove()で弾かずcheck()で弾いているのは開始時点は外周から始まるためです。
上記いずれでもない場合、分割できていないので0を返します。
count()
上辺、左辺のいずれかから開始した場合に2分割できるパターン数を求めます。
引数queueには上辺、左辺の開始位置の状態が入っています。
queueがからになるまで処理を行います。
queueから先頭の要素を取り出し、Grid#move()で次の状態のリストを取得します。
リストの各状態をGrid#check()でチェックし、1ならパターン数をインクリメントし、0なら継続探索としてqueueに追加します。-1の場合は無効なパターンなので何もせず無視します。
queueがからになった時が結果なのでパターン数を返却します。
雑感
私は交点を辿るロジックにしましたが、マスを辿ってもできると思います。
ただ、マスを辿る場合、単純に最後に到達したマスに隣接するマスを処理することができない(例図の左上のパターンの場合を考えると一筆書きでぬりつぶせない)ので交点を辿る方が簡単と思います。