CodeIQ：ウッド・キーパー

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「ウッド・キーパー」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

n 本の丸太があります。これらの向きと端をそろえ、地面に積みます。

積む際には次のルールに従います。

地面には好きな本数の丸太を置けます。隣り合う丸太は接して置きます。
左右に隣り合う 2 本の丸太の上に、新たな丸太を 1 本置けます。
全ての丸太は一つながりになっていないといけません。

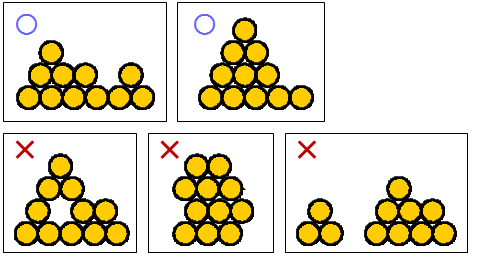
n＝11 のときの置き方をいくつか示します。
横から見た図です。上の 2 つは正しい置き方ですが、下の 3 つは正しくない置き方です。

n 本の丸太の可能な置き方の総数を F(n) と定義します。
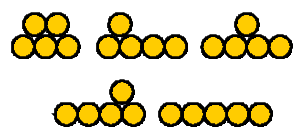
例えば F(5)＝5 です。可能な置き方を以下に示します。

同様に、F(1)＝1, F(3)＝2, F(4)＝3, F(11)＝135 となることが確かめられます。

標準入力から、自然数 n （1 ≦ n ≦ 60）が与えられます。
標準出力に F(n) の値を出力するプログラムを書いてください。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

# A005169
def f(n,x)
	return $Memo[[n,x]] if $Memo[[n,x]] != nil

	ret = 0
	if x > n then return 0
	elsif x == n then return 1
	else
		for y in 1..(x+1)
			ret += f(n-x, y)
		end
	end

	$Memo[[n,x]] = ret
	return ret
end

# main
while line = gets
	line.strip!
	next if line.empty?

	p f(line.to_i, 1)
end

解説

私には数学が足りないので早々に自力で考えるのをやめました。。

考え方

最初に書いた通り早々に自力で考えるのをやめたので考え方というのはありません。
問題を読んですぐに、これはOEISにあるだろうな、ということだけは予測がつきました。

F(6)くらいまでなら手でパターン数を求めるのも容易なので、パターン数を手動で求めOEISで検索しました。何パターンか見つかりますが、F(7)を追加で数え、さらにF(11)が一致するものはA005169だけだったので、そのFomulaの最初の式を実装しました。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

f(n,x)

以下の式の通りです。
Rubyではpという関数があるのでxに変えました。

A005169(n) = f(n, 1), where f(n, p) = 0 if p > n, 1 if p = n, Sum(1 <= q <= p+1; f(n-p, q)) if p < n.

雑感

一応、メモ化再帰で真面目にパターンを作ってゆく実装はできそうですがn=60とかは絶対に時間切れになると思います。つまり、漸化式を導かないと無理というわけで考えるのをヤメました。
上記の実装ですらメモ化しないと時間切れになります。

問題では丸太を積んでいますが、OEISではコインでした（どうでもいいですが）。