CodeIQ：素因数分解で和が同じ

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「照明を消さずに端から端まで移動」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
夜、家に帰ったら真っ暗。暗い部屋を移動するのは大変です。
そこで、室内の照明をオン・オフするスイッチが複数個所に設置されていることは珍しくありません。
例えば、廊下の電球などの場合、玄関とリビングなどのどちらでも切り替えが可能になっています。

そこで、少なくとも一つの照明をつけたまま移動することを考えます。
今回は n 個の照明が一列に並んでいるものとします。
それぞれの照明は、向かい合うスイッチと両隣のスイッチで操作できます。

最初に左端の照明だけを点灯した状態でスタートし、右端の照明だけを点灯した状態にするまで、それぞれのスイッチを操作します。
ただ、一つのスイッチを操作すると、その正面と両隣にある照明もオン・オフが切り替わります。
（左端と右端のスイッチは正面の照明と、その隣りにある照明だけが切り替わります）

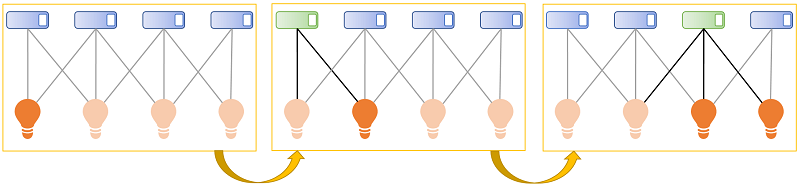
例えば、n = 4 のとき、以下のような4つのスイッチと4つの照明があるとします。
左端のスイッチを押すと、左端の2つの照明が切り替わり、2つ目の照明だけが点灯します。
次に右から2つ目のスイッチを押すと、図のように3箇所が切り替わるため、右の2つが点灯します。
この場合は、まだ右端だけが点灯した状態にはなっていません。

fig.1

n = 4 のとき、最初に左から2番目のスイッチを押し、次に右から2番目のスイッチを押すと、いずれかの照明が点灯したまま、右端の照明だけを点灯するようにできます。
つまり、最短で2回スイッチを押すと、目的を満たすことができます。

標準入力から n が与えられたとき、最短の手順を求め、スイッチを押した回数を標準出力に出力してください。
なお、n は 2≦n≦16を満たす整数とします。

【入出力サンプル】
標準入力
4

標準出力
2

私のプログラム

Rubyで解答しています。

$Memo = {}

def switchLight(now, mask, sw)
	lt = 0
	if sw == 0 then lt = 0b11
	else lt = mask & ((0b11 << sw) | (1 << (sw-1)))
	end

	#printf("now=%05b, mask=%05b, sw=%d, lt=%05b, ret=%05b\n", now, mask, sw, lt, now ^ lt)
return mask & (now ^ lt)
end

def solve(n)
	st = 1
	ed = 1 << (n-1)
	mask = 0
	for i in 0...n
		mask |= 1 << i
	end

	$Memo[st] = true
	queue = [st]
	cnt = 1

	while true
		nq = []

		for q in queue
			for i in 0...n
				r = switchLight(q, mask, i)
				if $Memo[r] then next
				elsif r == ed then return cnt
				else
					nq << r
					$Memo[r] = true
				end
			end
		end

		cnt += 1
		queue = nq
	end
end

# main
while line = gets
	line.strip!
	next if line.empty?

	p solve(line.to_i)
end

解説

この出題者の問題の中では簡単な方と思います。

考え方

問題通り、左の明かりだけが点いている状態で始めて、任意のスイッチを押し、また任意のスイッチを押す、という操作を総当たりでやればできます。

ポイントは最短手数を求めるということで、全てのパターンを求める必要はありません。なので、手順1回目、2回目、……、と回数ごとに操作を行い、最初に条件を満たした時点でやめれば十分です。

後、計算を簡単かつ高速に行うためビット演算を使用します。
つまり、明かりがついている場所を1、ついていない場所を0として表現し、最初は最下位ビットだけが1の状態で入力値-1ビット目だけが1になれば終了とします。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(n)

stは初期状態で最下位ビットだけが1になっています。
edは終了状態で入力値-1ビット目だけが1になっています。
$Memoは同じ状態を省くために使用し、キーが明かりの状態で値はtrueになります。初期状態は最初から存在するので$Memoに追加しておきます。
queueは途中状態の明かりの状態を全て保持しておくための配列です。

queueから状態を1つ取り出し、switchLight()で任意のスイッチを押します。29行目のforループのカウンタiがスイッチの場所を示します。
スイッチを押したら明かりの状態が返ってくるので、$Memoにその状態があるかをチェックします。あった場合、状態の繰り返しになるので無視します。
なかった場合、終了状態になっているかをチェックし、終了状態ならぉのときのcntを返却して終了します。cntは何回目かを表すカウンタです。
終了状態になっていなければnqに状態を追加します。

queueが空になったらcntをインクリメントし、nqをqueueと置き換えて処理を繰り返します。

switchLight(now, mask, sw)

スイッチを押した時の明かりの状態を計算します。
引数nowは現在の状態、maskは明かり（スイッチ）の数だけビットに1を立てたもの、swは押すスイッチの場所です。
ltはsw番目のスイッチを押した時に点灯する明かりをビット表現したものです。

5行目は左端のスイッチを押した場合に点灯すべき場所を設定します。
6行目はそれ以外の場所の場合で、右端の場合にはみ出してしまうのでmaskで不要な部分を0にしています。

スイッチを押した時の状態はnowとltの排他的論理和になるのでその値を返します。

雑感

ちょっと珍しいタイプ（全パターンやらなくても良い）の問題だったような気がします。
私は最初に（仕事で使えるレベルで）習得した言語がC言語なこともあってビット演算は結構好きです。RubyとかPythonの場合でもビット表現できると配列に比べて簡単に計算できますし、配列のコピーをしなくても良いので楽です。