CodeIQ：ホーム画面を整理して！

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「ホーム画面を整理して！」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
多くの人が使うようになったスマートフォン。
そのホーム画面には多くのアプリのアイコン（以下、アイコン）が並びます。
そこで、このアイコンをフォルダにまとめて整理することを考えます。

1つのフォルダには2個～9個のアイコンを登録でき、登録するとフォルダ1つのアイコンにまとまり、そのフォルダに登録されているアイコンの数が識別できるようになります。
なお、フォルダの中にフォルダを作ることはできません。

n 個のアイコンを整理するとき、そのフォルダ構成について、アイコンの数の組み合わせがいくつ考えられるかを求めます。
ただし、個々のアイコンは識別せず、並び順も考えないものとし、アイコンの数の組み合わせだけを考えます。
（フォルダ内にあるアイコンの数が異なる場合は、別々のフォルダ構成としてカウントします。）
なお、ホーム画面には最大で24個のアイコンを並べられるものとし、n は 1≦n≦216を満たす整数とします。

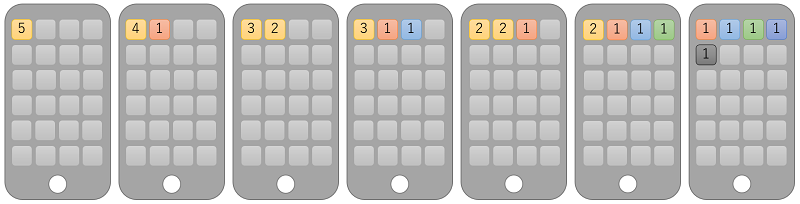
例えば、n = 5 のとき、以下の7通りがあります。
（図の黄色はフォルダを、数字はアイコンの数を表します。）
当然、n = 216のときは、すべてフォルダにまとめた1通りしかありません。
fig.1

【入出力サンプル】
標準入力
5

標準出力
7

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

$Memo = {}

def solve(n, st, d)
	if 24 < d then return 0
	elsif n == 0 then return 1
	elsif n < 0 then return 0
	elsif $Memo[[n,st,d]] != nil then return $Memo[[n,st,d]]
	end

	ret = 0
	for i in st..9
		ret += solve(n-i, i, d+1)
	end

	$Memo[[n,st,d]] = ret
	return ret
end

# main
while line = gets
	line.strip!
	next if line.empty?

	p solve(line.to_i, 1, 0)
end

解説

よくあるメモ化再帰の問題でした。

考え方

単純に入力値nからフォルダに入れるアイコン数1〜9を引き、残りに対して、引いた数以上の数を同じように引く、という操作をnが0になるまで繰り返すだけです。
ただし、フォルダ数は最大24個という制限があるので操作回数（＝フォルダ数）を考慮する必要があります。

main

入力値を数値にしてsolve()に渡し、結果を印字します。

solve(n, st, d)

引数は次の通りです。
nは残りのアイコン数です。
stはフォルダに入れるアイコン数の最小値です。
dは操作回数（=フォルダ数）です。

12〜15行目の処理でフォルダに入れるアイコン数を決定し、残りのアイコンに対してsolve()を再帰呼び出ししています。次のフォルダに入れるアイコン数はその時フォルダに入れたアイコン数で、これによって重複を無くします。dは呼び出しごとにインクリメントします。

6〜10行目は終了条件です。
操作回数が24を超えたらフォルダに入れられないアイコンがあるのでダメです。
それ以外でnが0になった時は正しく割振れているので1を返します。
n&lr;0の時はアイコンが足りなくなっているのでダメです。

あとは高速化のためメモ化しています。キーはsolve()の引数でパターン数が値です。9行目ではすでに計算済みのパターンがあれば結果だけを返しています。

雑感

よくあるパターンの問題なのでサクッと終わりました。
ただ、最初フォルダ数の最大値を見落としていてダメでしたが。