CodeIQ:正方形の分割
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「正方形の分割」(CodeIQ)を参照してください。
問題の概要
【概要】
正方形があります。
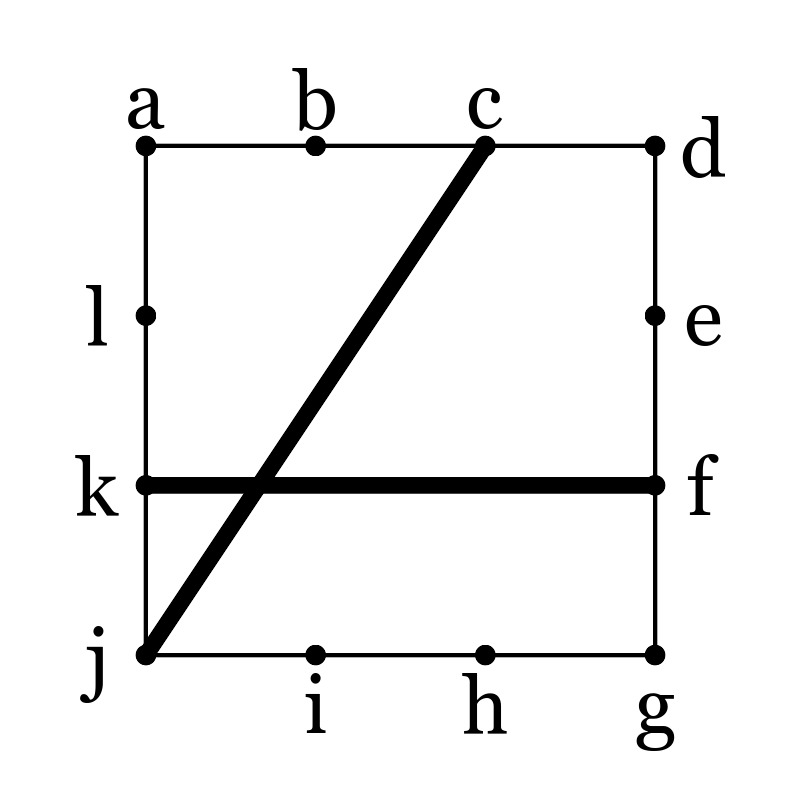
正方形の頂点と、辺の三等分点を全部合わせて「注目点」と呼びます。
注目点のうちのひとつを別の注目点と結んだ線分で、正方形を分割する、という操作を2回行います。
このとき、出来る図形が何角形になるのかを計算して下さい。
【入出力】
入力は
cj kf
のようになっています。
線分を示す文字列が 空白区切りで並んでいます。
線分を示す文字列は、右図にある端点を示す記号をならべたものです。
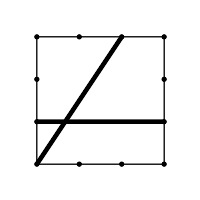
というわけで、cj kfは、右上図の黒い線の部分での分割を意味します。
出力は、
3,4,4,4
のような感じです。
出来上がる多角形の頂点数を、昇順にコンマ区切りで。
くれぐれも、昇順にソートすることをお忘れなきよう。
【例】
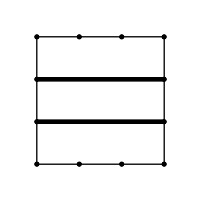
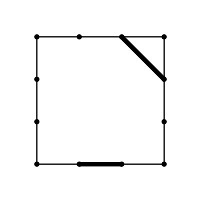
入力 出力 状況 cj kf 3,4,4,4 kf el 4,4,4 ce ih 3,5
【補足】
不正な入力に対処する必要はありません。
「ih」のように何も分割しない線分が入力に含まれる場合があります。
内角が180度の点は頂点ではなく、辺の途中です。
入力に含まれる線分は 2 本 です。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# true: 交差する
# false: 交差しない(1点を共有する場合も)
def cross(a, b)
return false if (a[0] == b[0]) || (a[0] == b[1]) || (a[1] == b[0]) || (a[1] == b[1])
ret = 0
for x in (a[0]+1)...a[1]
ret += 1 if b.include?(x)
end
return ret == 1
end
def onEdge(l)
edge = [[0,1,2,3], [3,4,5,6], [6,7,8,9], [9,10,11,0]]
for e in edge
return true if e.include?(l[0]) && e.include?(l[1])
end
return false
end
# pointsに含まれ、l[0]とl[1]の間にある点の番号を取得する(lに含まれる点は含む)
def cutPoints(points, l)
ret = []
for x in l[0]..l[1]
ret << x if points.include?(x)
end
return ret.sort
end
# cutPointsで切り取った残りの点を取得する。
# lとcuttedに含まれる点は残す
def restPoints(points, cutted, l)
ret = points - cutted
ret << l[0] if cutted.include?(l[0])
ret << l[1] if cutted.include?(l[1])
return ret.sort
end
def joinEndPos(arr)
ret = arr.dup
if (ret.first == 0) && (ret.last == 11) then
buf = ret[0]
ret[0] = 12
for i in 1...ret.size
break if ret[i] > buf+1
buf = ret[i]
ret[i] += 12
end
end
return ret.sort
end
# 範囲内で正方形の辺が分割されている場合、連続している領域ごとの配列を返す
# 2以上の領域には分割されない
def getSplited(arr)
buf = arr[0]
for i in 1...arr.size
if arr[i] != buf+1 then
return [arr[0...i], arr[i..-1]]
end
buf = arr[i]
end
return [arr]
end
def countCorner(arr)
return 1 if arr.size == 1
ret = 2
for i in 1...(arr.size-1)
ret += 1 if arr[i] % 3 == 0
end
return ret
end
def getPolygon(arr, crossed)
ret = 0
splited = getSplited(arr)
for s in splited
ret += countCorner(s)
end
ret += 1 if crossed
return ret
end
def solve(a, b)
lines = []
if a == b then
lines << a if !onEdge(a)
else
lines << a if !onEdge(a)
lines << b if !onEdge(b)
end
# 全ての線が四角形の返上にある場合、元の四角形だけ
return [4] if lines.size == 0
# 1本目の線で分割
if lines.size >= 1
ps1 = []
ps1 << cutPoints((0..11).to_a, lines[0])
ps1 << restPoints((0..11).to_a, ps1[0], lines[0])
end
# 2本以上の線で分割される場合
ps2 = []
if lines.size == 2
for ps in ps1
p1 = cutPoints(ps, lines[1])
p2 = restPoints(ps, p1, lines[1])
ps2 << p1
ps2 << p2
end
else # 線が1本の場合
ps2 = ps1
end
# 分割した線をlとaの場所が繋がるなら繋ぐようにする
# 同時に多角形を作れない要素を除く
points = []
for ps in ps2
next if ps.empty? || (ps.size == 1)
points << joinEndPos(ps)
end
ret = []
crossed = cross(a, b)
for ps in points
ret << getPolygon(ps, crossed)
end
return ret.sort
end
# main
while line = gets
line.strip!
next if line.empty?
a, b = line.split.map{|l| l.split("").sort.map{|c| c.ord - "a".ord}}
puts solve(a, b).join(",")
end
解説
★★★の問題です。
結構難しい上に面倒臭いです。
考え方
線が正方形の内側で交差する場合をベースとして考えます。
この場合、a〜lにできた線と正方形の交点のうち隣り合うものを2つ選び、線と正方形の交点を含まずに、その間にあるa~lのうち角にあるもの(a,d,g,j)を数え、+3したものが答えになります。
例1を見ると(c,f)の間にはdがあるので1+3=4、(f,j)の間にはgがあるので1+3=4(交点は含まないのでjをカウントしない)、(j,k)の間には角がないので3、(k,c)の間にはaがあるので1+3=4というわけです。
線が交わらない場合(例2のような場合)を考えてみます。
これで問題になるのは[e,f,k,l]でできる領域です。ベースの考え方のように隣り合う2つの交点の間に含まれる点で考えることができないからです。
つまり領域に含まれる点をうまく分ける必要があります。
そのため、正方形の分割を2段階にします。
まず、[l,e]で正方形を2つに分割します。[l,a,b,c,d,e]と[e,f,g,h,i,j,k,l]になります(それぞれの領域に交点を含めます)。
次にそれぞれの領域を[k,f]で分割します。
[l,a,b,c,d,e]にはkが含まれないので分割できません。なので[l,a,b,c,d,e]のままです。
[e,f,g,h,i,j,k,l]は[k,f]の間にある点とそれ以外に分け、[f,g,h,i,j,k]と[e,f,k,l]になります。
結果として[l,a,b,c,d,e]、[f,g,h,i,j,k]、[e,f,k,l]になりうまく分割できます。
このうち[l,a,b,c,d,e]、[f,g,h,i,j,k]はベースの考え方と同じように交点の間にある角を数えます。領域の中にある角の数を考えると2個なので4=2(角の数)+2(交点)ということになります。
ここで一旦ベースの考え方を見直すと、正方形の内部に交点を持つ場合は多角形=角の数+交点(2)+線が交差するなら1、しないなら0、ということになります。
さて、この場合で問題は[e,f,k,l]の方です。同じようにするとここには正方形の角を含みません。しかし、[[e,f], [k,l]]の2つに分断されているので交点が4個あります。これをどう判断するかです。
これは点が連続しているかどうかで判断できます。点が連続していない場合、連続している部分だけを取り出し、それぞれについて前述と同じように考えます。この場合、[e,f]の間には交点0で交差していないので角は2個、[k,l]も同様に2個なので角の数は4個になります。
これを実現するためには[l,a,b,c,d,e]のような時にlとaが繋がっていると判断しなければなりません(コードの説明参照)。
四角形の辺と線の交点が作る角に1つ例外があります。それは四角形の辺上で交点を共有する場合です。例えば入力値が「bj bh」のような時(この場合はbを共有している)です。この場合、角は1つしかできないのでこれを判断する必要があります。
以上が大体の考え方です。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
入力値はaを0、lを11の数値に変換し、ソートして渡します。
solve(a,b)
問題を解きます。
引数a,bはそれぞれ線の開始点と終了点の番号の配列です。入力値が「cj kf」ならa=[2,9]、b=[5,10]です。
110〜115行目は同じ線が重なって引かれていればaだけ、そうでなければ両方を採用するという処理です。加えてonEdge()は正方形の辺上に線が引かれているなどうかを判断し、辺上にあるなら採用しないという判断をしています。
117行目は正方形が分割されていない(線が全て辺上にある)場合で、この場合は元の正方形1つだけなので[4]を返却して終了します。
121〜125行目で正方形を1つめ線で分割します。
cutPoints()で正方形の辺上の点を2つに分割します。例の場合だと[0,1,2,3,4,11]と[5,6,7,8,9,10]が返却されます。
[5,6,7,8,9,10]の方に[4,11]を含まないのでrestPoints()で調整します。
128〜139行目は2本目の線での分割です。
129行目の条件は、入力値の線が両方とも正方形を分割している場合で、elseは一方の線が正方形の辺上にある場合です。elseの場合は2本目の線での分割が必要ないので2回目の分割を行った結果を1回目の分割の結果とします。
130〜136行目は1回目の結果で得られた2つの領域をそれぞれ2本目の線で分割します。
143〜147行目の処理は139行目までで得られた分割された領域の点が連続しているなら連続しているように調整する処理です。
例えば[0,1,2,3,4,11]を[11,12,13,14,15,16]にします。
同時に領域が多角形を作れない場合を排除します。
150行目の処理は線が正方形の内側で交差しているかどうかをチェックします。
151〜153行目の処理で多角形の形状を判定します。
結果をソートして返却します。
onEdge(l)
引数lは線の始点と終点の値の配列です。
始点、終点共に一つの辺上に暑場合、辺上にあると判断します。
cutPoints(points, l)
pointsは正方形の辺上の点の集合です。
lは正方形を分割する線の始点と終点の番号です。
これはl[0]〜l[1]の間の値がpointsにあればその番号を返却値とします。
restPoints(points, cutted, l)
cutPoints()で切り取った残りの点の集合を求めます。
pointsはutPoints()で切り取る前の点の集合です。
cuttedはcutPoints()で切り取った点の集合です。
lは正方形を分割する線の始点と終点の番号です。
これはpointsとcuttedの差集合をとり、cuttedにlの番号が含まれていれば結果に加えます。
43〜44行目の条件は2回目の分割のためです。例の場合で[0,1,2,3,4,11]を[5,10]で分割した場合、5(fの番号)は含まれますが10(kの番号)は含まないのでそれを考慮した処理です。
joinEndPos(arr)
この関数はlとaが繋がるなら繋げる処理です。
引数arrは分割後の点の集合です。
lとaの部分で繋がるかどうかはarrが0と11の両方を含むかどうかで判断できます。
bufは連続性を判断するために一つ前の番号を保持しておきます。
arrはソートされているので前から順にチェックしてゆき連続している間元の値に12を加えます。これで連続した番号にできます。
例えば[0,1,2,3,4,11]の場合だと0〜4まで連続しているので[12,13,14,15,16,11]になり、ソートして[11,12,13,14,15,16]が結果として返却されます。
cross(a, b)
aとbの2つの線が交わっているかを判断します。
正方形の辺上で点を共有している場合は交差していないと判断します。
6行目は交点を共有しているかどうかです。
それ以外の場合、aの始点と終点の間にbの始点か終点があれば交わっています。
getPolygon(arr, crossed)
arrは分割後の正方形の辺上の点の集合です。
crossedは線が正方形の内側で交差しているかどうかです。
96行目はarrが全て連続していない場合、連続している部分ごとに集合を分割して取得します。
98〜100行目でgetSplited()で得られた部分ごとに角を数えます。
例えば[4,5,10,11]の場合[4,5]と[10,11]をgetSplited()で分け、それぞれに対してcountCorner()で角の数を数えて合計します。
最後に線が交差している場合、1を加えて返却します。
getSplited(arr)
arrは分割後の正方形の辺上の点の集合です。
これはarrのうち連続している部分をチェックし、途中で途切れていた場合、それより前とそれ以降に分けて返します。そうでなければarrだけを含む配列を返します。
問題の条件からarrが3以上に分割されている可能性はないので2つに分割することだけを考えれば十分です。
countCorner(arr)
arrの点の中に正方形の角があればその数を数えます。
正方形の角は3の倍数になるのでそれをチェックします。
雑感
コードも長いですが結構大変でした。ただ、頑張ればできる感じの問題ですが。
ちなみに、この問題の最初の正解者でした。