CodeIQ:素数の日付を含む最長期間
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「素数の日付を含む最長期間」(CodeIQ)を参照してください。
問題の概要
日付をYYYYMMDD形式で表現し、8桁の数値としてみたとき、その値が素数かどうかを判定します。
1970年1月1日~2019年12月31日までの50年間のうち、素数がちょうど n 個含まれる期間で最長のものを考え、その日数を求めます。
なお、日数は両端の日付を含んで数えるものとします。
また、閏年は考慮するものとします。
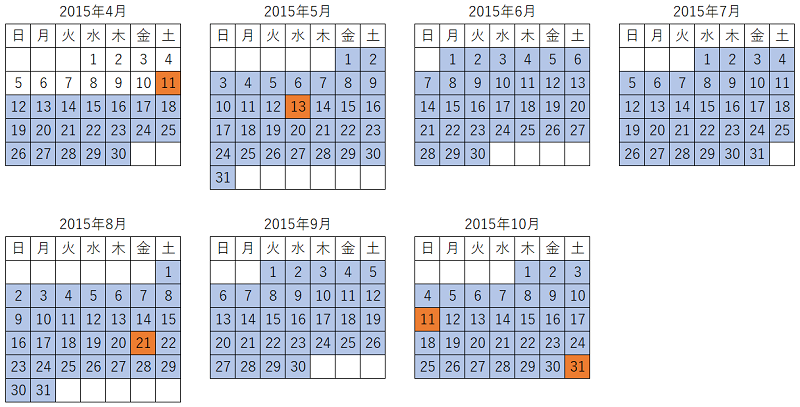
例えば、n = 3 のとき、以下の青色で塗りつぶした範囲が最長になり、その日数は「202」です。
2015-04-11 : 素数
2015-04-12 : 開始日
2015-05-13 : 素数
2015-08-21 : 素数
2015-10-11 : 素数
2015-10-30 : 終了日
2015-10-31 : 素数
標準入力から n が与えられたとき、その最長日数を求め、標準出力に出力してください。
なお、n は1000以下の自然数とします。
【入出力サンプル】
標準入力
3
標準出力
202
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
Days = {
1 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
2 => [1,3,7,9,11,13,17,19,21,23,27,29],
3 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
4 => [1,3,7,9,11,13,17,19,21,23,27,29],
5 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
6 => [1,3,7,9,11,13,17,19,21,23,27,29],
7 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
8 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
9 => [1,3,7,9,11,13,17,19,21,23,27,29],
10 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
11 => [1,3,7,9,11,13,17,19,21,23,27,29],
12 => [1,3,7,9,11,13,17,19,21,23,27,29,31],
}
# 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
LastDays = [0 , 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31]
def modPow(base, power, mod)
ret = 1
while power > 0
ret = (ret * base) % mod if power & 1 == 1
base = base**2 % mod
power >>= 1
end
return ret
end
# フェルマーテストで素数判定
# 2と3をテストすればPrime.prime?の結果と一致する
def makePrimeDays()
ret = []
for y in 1970..2019
for m in 1..12
if (m == 2) && ((1 / (y % 4 + 1)) * (1 - 1 / (y % 100 + 1)) + (1 / (y % 400 + 1)) != 1)
ds = Days[m][0..-2]
else
ds = Days[m]
end
for d in ds
v = 10000 * y + 100 * m + d
next if (v % 3 == 0) || (v % 7 == 0)
next if modPow(2, v-1, v) != 1
next if modPow(3, v-1, v) != 1
ret << v
end
end
end
return ret
end
def countDays(f, l)
# printf("%d %d\n", f, l)
fy = f / 10000
fm = (f - 10000 * fy) / 100
fd = (f - 10000 * fy - 100 * fm)
ly = l / 10000
lm = (l - 10000 * ly) / 100
ld = (l - 10000 * ly - 100 * lm)
ret = LastDays[fm] - fd
ret += (1 / (fy % 4 + 1)) * (1 - 1 / (fy % 100 + 1)) + (1 / (fy % 400 + 1)) if fm == 2
y = fy
m = fm + 1
if m == 13 then
y += 1
m = 1
end
# printf("%d/%d, %d, %d\n", fy, fm, ret, ret)
while (100*y+m) < (l/100)
d = LastDays[m]
d += (1 / (y % 4 + 1)) * (1 - 1 / (y % 100 + 1)) + (1 / (y % 400 + 1)) if m == 2
ret += d
# printf("%d/%d, %d, %d\n", y, m, d, ret)
m += 1
if m == 13 then
y += 1
m = 1
end
end
ret = ret + ld - 1
# printf("%d/%d, %d, %d\n", ly, lm, ld-1, ret)
return ret
end
def solve(n)
days = makePrimeDays()
days.unshift(19691231)
mx = 0
for i in (n+1)...days.size
v = countDays(days[i-n-1], days[i])
mx = v if v > mx
end
return mx
end
# main
while line = gets
line.strip!
next if line.empty?
p solve(line.to_i)
end
解説
一応正解はしていますが指定される期間が変わると私のコードは正しい答えが出なくなる可能性があります。
考え方
問題は素数判定です。RubyにはPrime#prime?という素数判定関数があるのですが、やって見たら時間的に間に合いません。一度求めた素数はキャッシュしているらしく、2つ目からは非常に早いのですが、最初の1つに1秒以上かかってしまいます。
ということでフェルマーテストを利用しました。
これはある数nに関して、an-1 mod n(aはnと素な任意の数)の答えが1以外ならnは合成数である、というもので、これを利用して素数ならan-1 mod n = 1になるというものです。
ただし、疑素数の問題があります。
なのでa=2,3の2パターンでテストして篩に掛けることにしました。これはPrime#prime?の結果と一致するのでそうしたというだけなので、期間が変わると正しい答えが得られなくなる可能性があります。
期間の判断は入力値nの前後の素数になる日付を選び、両端を含まない期間を計算すればOKです。これは問題の図と説明を見れば簡単にわかります。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
定数Daysは各月の日のうち2の倍数と5の倍数を除いたものです(2月は閏年の2月に合わせています)。日が2の倍数と5の倍数の場合はYYYYMMDDでも絶対素数にならないため計算量を減らすためあらかじめ除いています。
LastDaysは各月の最後の日(閏年を考慮しない)です。
solve(n)
makePrimeDays()で素数になる日を列挙します。
先頭に19691231(開始日の1日前)を追加します。20191231(最後の日)はたまたま素数なので追加していませんが、素数でなければ20200101を追加する必要がありました。これは期間の計算を統一するためです。
106〜110行目では総当たりで期間の日数を計算し、最大値を選んでいます。
最終的に最大値を返却します。
makePrimeDays()
素数になる日付をYYYYMMDD形式の数値で列挙します。
年月日の3重ループでYYYYMMDDの値を作っています。
40行目は2月の場合、閏年ならDays[2]の最後の要素を含まないことで29日を省くという処理です。
49行目と50行目でフェルマーテストにかけて合成数を除き、それ以外の数を素数としています。
ちなみに19700101〜20191231の間の素数は1099個で、49行目をパスするのは1100個です。
modPow(base, power, mod)
これは冪剰余を計算するための関数です。
フェルマーテストはan-1 mod nですが、普通に2**(n-1)%nのような計算をするとnが8桁もあるため計算できないのです。この関数はWikipediaあたりの解説を見てください。
countDays(f, l)
引数f、lはそれぞれ日付のYYYYMMDD形式の数値表現で、f〜lまでの日数(f, lを含まない)を計算します。
62〜64行目で開始日、66〜68行目で終了日を年月日それぞれの数値に分割しています。
70行目で最初の月の日数を返却値の初期値としています。最初の月に含まれる日数は「その月の日数(=最終日)-開始日」で計算できます。71行目は閏年の2月の処理です。
96行目は最後の月の日数の加算で、これは終了日の日付-1日になります。
80〜94行目のループは最初の月と最後の月以外の月の日数の加算処理です。これらの月は必ず全日加算されるのでその処理を行います。
73〜78行目と89〜93行目の処理は年の繰り上がり処理で、13月になったら翌年1月にするという計算をしています。
最終的に期間の日数を返却します。
雑感
フェルマーテストでごまかしましたが、本当はどうするんでしょうか?
エラトステネスの篩が√(最終日)までだから、最終日の1/2乗以下の素数を列挙しておいてそれで計算するで間に合うのでしょうか?