CodeIQ:正六角形の分割
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「正六角形の分割」(CodeIQ)を参照してください。
問題の概要
【概要】
正六角形があります。
正六角形の頂点と、辺の中点を全部合わせて「注目点」と呼びます。
注目点のうちいくつかを正六角形の中心と結んだ線分で、正六角形を分割します。
このとき、出来る図形が何角形なのかを計算して下さい。
【入出力】
入力は
69
のようになっています。
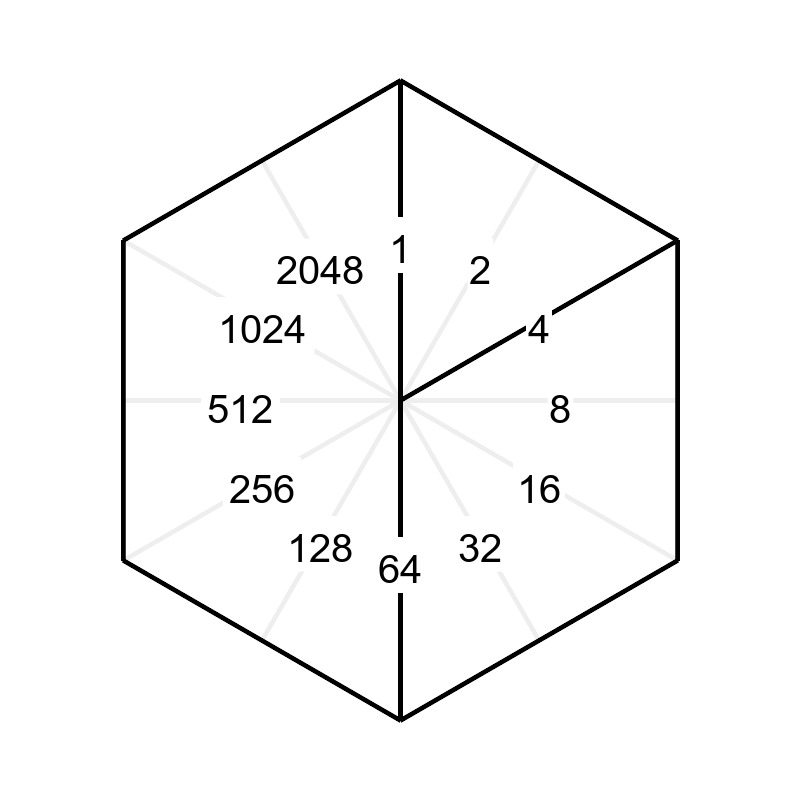
これは、線分に割り当てられた値(右図参照)の合計です。
69=1 + 4 + 64
なので、右上図の黒い線の部分で分割されます。
出力は、
3,4,4
のような感じです。
出来上がる多角形の頂点数を、昇順にコンマ区切りで。
【例】
入力 出力 状況 69 3,4,4 57 3,3,4,6 1170 4,4,4,4
【補足】
不正な入力に対処する必要はありません。
少なくとも2箇所の注目点は、中心と結ばれます。
内角が180度の点は頂点ではなく、辺の途中です。
入力は 3以上 4095以下の整数です。
凹多角形になっても気にせず頂点数を数えて下さい。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def morePeaks(a,b)
ret = 0
for i in (a+1)...b
ret += 1 if i%2==0
end
return ret
end
def solve(n)
peaks = [];
11.downto(0){|i|
if n - 2**i < 0 then next
else
peaks << i
n = n - 2**i
end
}
peaks.reverse!
ret = []
for i in 0...peaks.size
a = peaks[i]
b = (i == peaks.size-1 ? 12+peaks[0] : peaks[i+1])
ret << morePeaks(a,b) + 2 + (a+6==b ? 0 : 1)
end
return ret.sort
end
# main
while line = gets
line.strip!
next if line.empty?
puts solve(line.to_i).join(",")
end
解説
ぱっと見結構難しそうかと思いましたがそうでもありませんでした。
考え方
六角形の中心からの線につけられた数字は2n(n≧0)なので、真上の線をn=0として単純に計算できます。
そして、六角形の外周上の任意の点を選択し、それが入力値以下ならその値を入力値から引いて選択した値より小さい数字を同様に処理し、0になるまで繰り返すことで入力値で選択された注目点の場所を確定することができます。
あとは隣り合う2点の間にある点の数+2(中心と注目点を結んだ線と六角形の外周の線で作られる頂点)と中心にできる頂点の合計が答えになります。ただし、2つの注目点の間が6の場合、中心に頂点ができないのでそれを考慮する必要があります。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n)
問題を解きます。
配列peaksは入力値から選択された注目点の番号(真上を0として1〜11)を保持します。
13〜20行目の処理で入力値で選択された注目点の番号を求めています。大きな番号から順にその注目点と中心の線につけられた値をnから引いてみて0未満にならなければ採用します。考え方に書いた通り線の番号は2注目点の番号で計算できます。
番号は大きな方から採番されるので小さい番号からに並び直します。
23〜28行目の処理で隣り合う2点を選んでその範囲の頂点数を数えます。
25行目の処理は最後の点は最初の点との組みになるのでその判定ですが、最初の点は12以上になるように計算しています。これはmorePeaks(a,b)で六角形の外周上の頂点を数える時a<bであることが条件なのでそのためです。
27行目でmorePeaks()で外周上の頂点を数え、注目点にできる頂点2を加え、中心と2つの注目点を結ぶ線が直線になっていなければ中心にできる頂点1を加えて答えとします。
最終的に頂点数の配列をソートして返却します。
morePeaks(a,b)
注目点a,bの間にある頂点数を数えます。
これは簡単でa,bの間にある偶数番号を数えればOKです。
雑感
最初、図形の問題で難しそうと思いましたがそんなことはありませんでした。