CodeIQ:ダイヤルロックを解除して!
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「ダイヤルロックを解除して!」(CodeIQ)を参照してください。
問題の概要
以下の図のようなダイヤル式のロックが付いたポストがあります。
このロックを解除するには、ダイヤルを左右交互に回転し、特定の m 桁の番号を作るとポストを開けられます。
なお、最初はダイヤルの位置が「0」にセットされているものとし、左回転から開始します。
(番号は「0」以外から始まり、同じ番号が続くことはありません。)
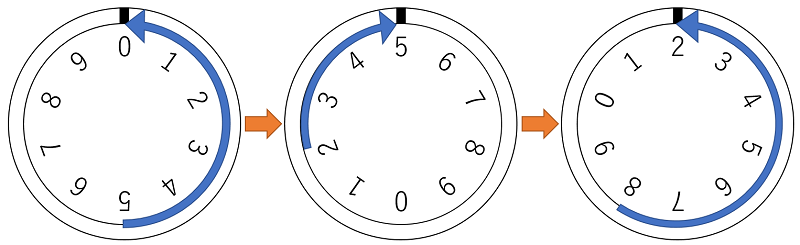
例えば、m = 3 で「528」という番号の場合、「5」まで左に回し、次に「2」まで右に回し、最後に「8」まで左に回します。
このときに動いた目盛りの数 n を考えます。
上記の「528」の場合、図のように n = 5 + 3 + 6 = 14 となります。
このポストを開けるとき、 m と n は覚えていたのですが、元の番号を忘れてしまいました。
そこで、このポストで m と n の数から番号を推測しようと考えました。
標準入力から m と n がスペース区切りで与えられたとき、考えられる番号が何通りあるかを求め、標準出力に出力してください。
なお、m と n は 0 < m < n < 50 を満たす整数とします。
例えば、 m = 3, n = 6 のとき、以下の10通りがあります。
「104」「178」「180」「192」「202」
「214」「290」「312」「324」「434」
【入出力サンプル】
標準入力
3 6
標準出力
10
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
$Memo = {}
def solve(m,n)
if $Memo[[m,n]] != nil then return $Memo[[m,n]] end
if n < m then return 0 end
if m == 0
if n == 0 then return 1
else return 0
end
end
mx = n - m + 1
mx = 9 if mx > 9
ret = 0
for i in 1..mx
ret += solve(m-1, n-i)
end
$Memo[[m,n]] = ret
return ret
end
# main
while line = gets
line.strip!
if line.empty? then next end
m,n = line.split.map{|a| a.to_i}
p solve(m,n)
end
解説
これも問題を読んだ瞬間、メモ化再起だなぁ、という問題です。
考え方
なので、(m,n)を引数にとる再帰関数を用意し、(m-1,n-1〜9)を再帰呼び出し時の引数として再帰関数を実行し、(m,n)=(0,0)になったパターンの数をカウントすればOKです。
後は高速化のため同じ計算を省くためにメモ化します。
メモはキーを(m,n)、値をその時のパターン数として用意すればOKです。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n, cnt, base)
再帰関数になっています。
n,mは残りの操作回数と移動量で、初期値は入力値です。
メモに結果があれば計算不要なのでその結果を返却して終わります。
m<nの場合、動かせない場合が出現するのでそれ以上計算する必要はなくNGなのでパターン数0を返却します。
m=0(最後の操作回数まで操作した)時にn=0ならロックが解除されるパターンなので1を返却します。n!=0ならNGなので0を返却します。
mxは目盛りの最大移動量です。mx=9が最大ですが、n-m+1が8以下ならそれより大きい数は試す必要がないので最大値を計算しています。
後は移動量iを1〜mxまでのパターンに対しsolve(m-1,n-i)を再帰呼び出しし、結果を加算します。
最終的に返却値の合計を返せば答えになります。
雑感
わかりやすい問題でした。ポイントはどの目盛りの履歴はもちろん、最後に目盛りに止まっているかも関係ない(=左右の移動も関係ない)ことでしょうか。
それはそうと、最近この出題者の問題にはメモ化再帰が多い気がします。