CodeIQ:上下反転した数字表示器
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「上下反転した数字表示器」(CodeIQ)を参照してください。
問題の概要
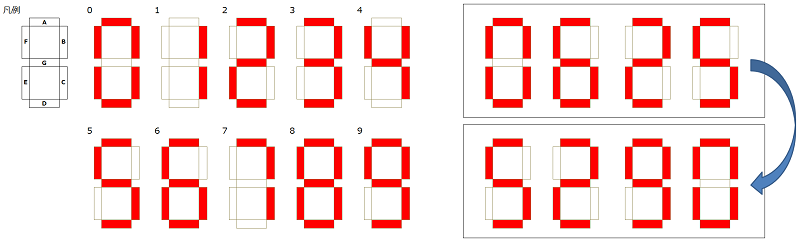
図のような7セグメントディスプレイを使った数字表示器があります。
この数字表示器を上下逆さに置いたとき、例えば「0625」は「5290」と読むことができます。
逆さに置いたときに対応する数字は以下のようになります。
0 <-> 0
1 <-> 1
2 <-> 2
5 <-> 5
6 <-> 9
8 <-> 8
(「1」は反転すると位置がずれますが、「1」として読み取ることが可能なものとします。)
n 桁を表示できる数字表示器を通常の置き方で置いた時よりも、上下逆さに置いた場合の方が大きな値として読み取ることができるものが何通りあるかを求めるプログラムを作成してください。
例えば、n = 2のとき、以下の21通りがあります。
01, 02, 05, 06, 08, 09, 12, 15, 16, 18, 19, 25, 26, 28, 29, 56, 58, 59, 66, 68, 86
標準入力から自然数 n が与えられますので、パターン数を標準出力に出力してください。
なお、n は最大で20とします。
【入出力サンプル】
標準入力
2
標準出力
21
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def solve(n, cnt, base)
# printf("cnt=%d, base=%d\n", cnt, base)
if cnt == n then return base end
if cnt == 0 then base = 1
elsif cnt == 1 then base = 7*(base+2)
elsif cnt % 2 == 0 then
a = base/7**(cnt/2-1)+1
base = 7**(cnt/2)*a
# printf("a=%d, base=%d\n", a, base)
else
a = base/7**(cnt/2)+2
base = 7**(cnt/2+1)*a
# printf("a=%d, base=%d\n", a, base)
end
return solve(n, cnt+1, base)
end
# main
while line = gets
line.strip!
if line.empty? then next end
p solve(line.to_i, 0, 0)
end
解説
コードは難しくありませんが、問題は難しいです。
パターン数が非常に多いので計算だけで解けるようにしないと時間切れは確実です。
考え方
まず、[0,1,2,5,6,8,9]で作れる数字のパターン数は全部で720あります。
列挙して問題通りにチェックしていては絶対に間に合いません。
答えの数字自体を効率よく作る方法を考えるにしろ、結果だけを計算するにしろ法則を見つけ出す必要があるのでとりあえず総当たりでやってみました。
結果、n=8までで次のようになります。
| n | 答え | パターン | 更にパターン |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 21 | 7*3 | 7*(1+2) |
| 3 | 154 | 7*22 | 7*(21+1) |
| 4 | 1176 | 7*7*24 | 72*(22+2) |
| 5 | 8281 | 72*169 | 72*(7*24+1) |
| 6 | 58653 | 72*7*171 | 73*(169+2) |
| 7 | 410914 | 73*1198 | 73*(7*171+1) |
| 8 | 2881200 | 74*1200) | 74*(1198+2) |
n=8の時点で1,000,000を超えているのでどんなに効率よくやっても実際に数値を作るのでは間に合いません。
ただし、答えのパターン数の計算に法則があるのがわかります。
nが偶数の時はn-1の場合の赤字部分+2、奇数の時はn-1の青字部分+1に7n/2(端数切り捨て)をかけた値になっています。
何でこうなるかはわかりませんが、この法則に従ってパターン数を求められると考えてプログラムにしました。
main
入力値を数値にしてsolve()に渡し、結果を印字します。
solve(n, cnt, base)
再帰関数になっています。
nは入力値、cntは何回目の操作か、baseは前回の結果です。
cntが0始まりなので注意してください。
cntがnに等しいなら答えがも止まっているのでbaseを返却します。
7〜17行目は考え方に書いた法則を実装しています。
cnt==0の時とcnt==1の場合を特別扱いして以降の計算の初期値としています(cnt==1の条件は不要にできたと思います)。
考え方の表の赤字、青字部分はn-1の結果から必要な回数7で割って求めて+1か+2し、必要な回数7を掛けて計算しています。
再帰呼び出しが返ってきたらそのまま結果として返却します。
雑感
うまく法則に気づけたのでできましたが諦めていてもおかしくなかった問題と思います。
一応真ん中の数字から左右に数字をつけて行く方法でも実際の値を作らずパターン数だけを数えることができそうなのですが、実装していないのでできるかどうかはちょっとわかりません。