CodeIQ:◯はぴったり☓は無し
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「◯はぴったり☓は無し」(CodeIQ)を参照してください。
問題の概要
【概要】
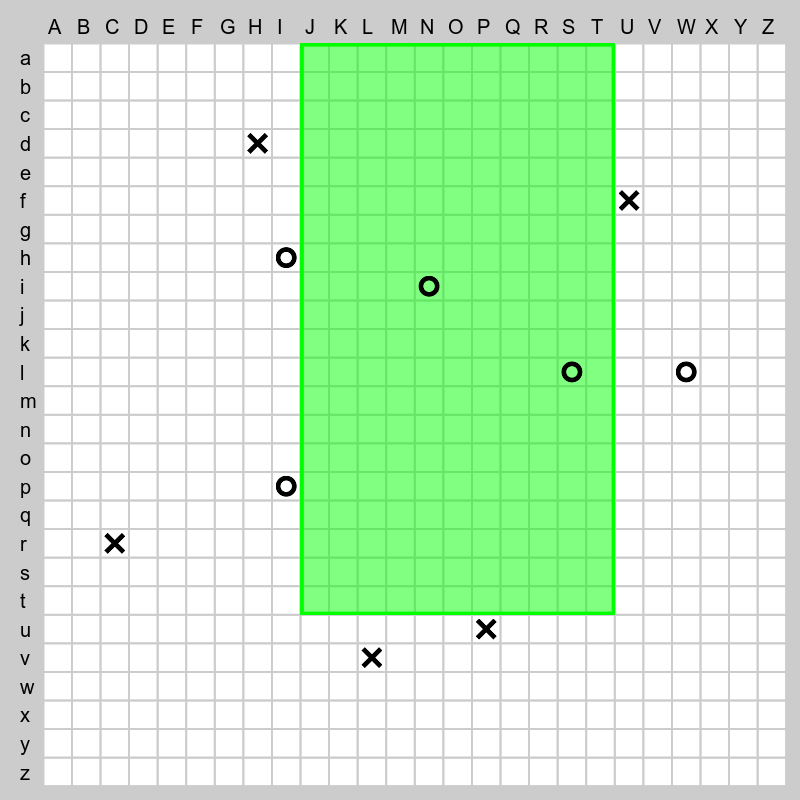
26×26のマス目に、◯と☓が配置されています。
数 n を指定します。マス目に沿った矩形のうち、◯をちょうど n 個含み、☓を含まない矩形として、最大となる矩形の面積を求めて下さい。
例えば、下図の場合、緑に塗られた部分が最大面積の矩形の例になります。
【入出力】
入力は、
2 Ip,Ni,Wl,Sl,Ih Cr,Lv,Pu,Uf,Hd
のようになっています。空白区切りで順に、n、◯のマスの座標、☓のマスの座標です。
一つ一つの座標はコンマで区切って並べられています。
座標は、x座標とy座標が区切り文字なしで並べられています。
(上記の入力が上図に対応しています)
出力は、
220
のように出力してください。
10進数で最大の面積を出力して下さい。
ただし、◯をちょうど n 個含み、☓を含まない矩形を作れない場合は
-
を出力して下さい。
【例】
入力 出力 状況 2 Ip,Ni,Wl,Sl,Ih Cr,Lv,Pu,Uf,Hd 220 7 Fl,Mi,Jl,Fp,Aq,Bm,Hn,Gz,Su,Fs Ul,Ko,Se,Xx,Jr,Xa,Wn,Jj,Hw,Zb - 2 Xm,Po,Kl,Dv,Ri,Zc,Lz,Yz,Ev,Ay Nh,Bc,Vc,Ok,Hm,Lw,Hz,Rv,Mv 184
【補足】
不正な入力に対処する必要はありません。
マス目に沿った矩形のみを考えます。つまり、傾いた矩形のことは考えません。
x 座標は大文字のアルファベット、y座標は小文字のアルファベットです。
◯の数、☓の数 は、いずれも 20 個を超えることはありません。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 入力値を座標に直す
# [x,y]
def parsePos(input)
ret = []
grids = input.split(",")
for g in grids
ret << [g[0].ord - "A".ord, g[1].ord - "a".ord]
end
return ret
end
# 矩形のリストを作成する
def getRects()
ret = []
for x in 1..26
for y in 1..26
ret << [x,y]
end
end
return ret.sort{|a,b| b[0]*b[1] <=> a[0]*a[1]}
end
# ×が含まれず○が丁度2個含まれるかチェックする
def check(n, st, rect, maru, batu)
ed = [st[0] + rect[0]-1, st[1] + rect[1]-1]
# printf("st=%s,ed=%s, rect=%s\n", st.to_s, ed.to_s, rect.to_s)
for b in batu
if ((st[0] <= b[0]) && (b[0] <= ed[0])) && ((st[1] <= b[1]) && (b[1] <= ed[1]))
return false
end
end
cnt = 0
for m in maru
if ((st[0] <= m[0]) && (m[0] <= ed[0])) && ((st[1] <= m[1]) && (m[1] <= ed[1]))
cnt += 1
end
if cnt > n then return false end
end
if cnt == n then return true
else return false
end
end
# 探索する
def search(n, rect, maru, batu)
for x in 0..(26-rect[0])
for y in 0..(26-rect[1])
if check(n, [x,y], rect, maru, batu) then return rect[0] * rect[1] end
end
end
return 0
end
# 問題を解く
def solve(n, maru, batu)
ret = 0
for rect in getRects()
if rect[0] * rect[1] < n then break end
ret = search(n, rect, maru, batu)
if ret != 0 then break end
end
if ret == 0 then return "-"
else ret.to_s
end
end
# main
while line = gets
line.strip!
if line.empty? then next end
input = line.split
n = input[0].to_i
maru = parsePos(input[1])
batu = parsePos(input[2])
puts solve(n, maru, batu)
end
解説
私は単純で簡単な方法をとりましたがああり効率が良いとは言えません。
考え方
考え方は非常に単純で、領域内でとり得る全ての矩形について、配置可能な全ての場所に対して条件を満たすところがあるかを調べるだけです。
領域内でとり得る矩形のパターンは676通りしかなく、最も小さい1×1の矩形でも676通りの配置しかないのでこの単純な方法でも間に合いそうです。ただ、多少は計算量を減らす工夫をします。
一つは大きな矩形から小さい矩形の順に調べることです。最大の面積なので見つかった時点でやめてしまえば良いわけです。
もう一つは矩形の面積が○の数より小さくなったら探索をやめることです。
main
入力値を分解し、○の数を数値、○と×座標を[[x,y],…]という配列にしてsolve()に渡し、結果を印字します。
parsePos(input)
○と×の座標を数値に変換します。
ASCIIなのでa〜zは文字コードにしてaの文字コードを引いた値、A〜ZはAの文字コードを引いた値が0始まりの座標になります。
solve(sum, mn, mx)
問題を解きます。
getRects()で面積で降順にソートした[[横,縦],…]の矩形リストを取得し、search()でその矩形が条件を満たす場所があるかを調べます。もし矩形の面積が○の数より小さくなったらそれ以上の探索は不要なのでブレークします。
retは最大の面積で0なら仕様通りに'-'を、そうでなければ数値を文字列化した値を返します。
search(n, rect, maru, batu)
引数nは○の数、rectは矩形([横,縦])、maruは○の座標リスト、batuは×の座標リストです。
矩形が配置可能な範囲の左上座標を1マスずつずらしながらcheck()で条件を満たす場所があるかをチェックします。条件を満たす場所があれば面積を返します。ループを最後まで処理した場合は見つからなかったことになるので0を返します。
getRects()
矩形を[[横,縦],…]の降順のリストで取得します。
一旦リストを作っているのは単純に二重ループで処理すると面積の順にならないからです。単純に降順の二重ループで生成した場合、[[26,26], [26,25], [26,24], …, [26,1], [25,26], …]となってしまいます。欲しいリストは[[26,26], [26,25], [25,26], [25,25], …]なので列挙してから面積でソートしてリストを作っているわけです。
check(n, st, rect, maru, batu)
引数nは○の数、stは矩形の左上座標、rectは矩形([横,縦])、maruは○の座標リスト、batuは×の座標リストです。
edは矩形の右下の座標で、stの座標とrectの値から計算できます。
×が含まれている場合はNGなので先に×の座標がst〜edの範囲にあるかをチェックします。もし見つかったらfalseを返却し処理を終えます。
領域内に×がなかったら○をチェックします。
cntは○の数を保持する変数です。
×の場合と同様にst〜edの範囲に○があるかを調べます。○の座標が範囲内にあればcntをカウントアップしますがcntが○の数より多くなった場合はNGなのでfalseを返却して処理を終えます。
両方の座標リストの途中でfalseを返却しなかった場合は○が入力値以下なので、cntをnと比較し丁度同じならtrue、そうでなければfalseを返却します。
雑感
他の方法も考えてみたのですがあまりうまく行きそうになかったのでほぼ総当たりのプログラムになりました。
考えてみた他の方法は3パターンです。
一つは○の座標から初めて矩形を大きくして行くという方法ですが、角の処理が厄介なのと、一段階前の矩形のリストから次のリストを生成するのが結構な回数になりそうで早くなさそうなのでヤメました。
二つ目は×を含まないで作れる矩形の領域をリストアップしてその中から○を指定数含む領域を探すというものですが、そもそも×を含まない領域をリストアップするのが難しく計算量も相当になりそうなのでヤメました。
三つ目は基本的に私の提出プログラムと同じですが、二分探査を組み合わせるという方法です。真ん中のサイズの矩形から始めて○が指定数以上か×を含んでいたら小さい方、そうでなければ大きい方を二分探査で調べるというわけですが矩形のパターン数が大したことないのでヤメてしまいました。でも、これが効率良かったかもしれません。座標のチェックは結構処理が重い(回数が多いので影響が大きい)のですが、一段階前に条件を満たしていた矩形を包含できない矩形は座標のチェックを省いて良いのが大きかった気がします。
とはいえ、私のプログラムでもCodeIQの実行環境で最悪のテストケースが0.2秒でした。私のプログラムの計算量は盤面の広さに依存するので、盤面が26×26より広くならない限りこれよりは大幅に遅くならないはずなのでそんなにマズくもないと思っています。