CodeIQ:幅優先の二分木を深さ優先探索
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「幅優先の二分木を深さ優先探索」(CodeIQ)を参照してください。
問題の概要
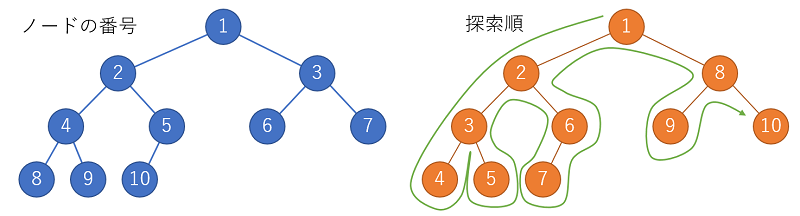
左図のように、ノードが左から順に埋まっている二分木を考えます。
この二分木に対し、根元の要素を「1」とし、幅優先で順番に番号を付与していきます。
(ノードの数が10個の場合は左図のような番号が付与されます。)
この二分木に対して、深さ優先探索を行います。
深さ優先探索では、左から順にもっとも深くなるまで進み、その後はバックトラックを行いながら順に探索します。
例えば、左図の場合は、右図のような順番に探索を行います。
m 個の要素が存在する二分木について、n 番目に探索したノードの番号を求めます。
例えば、m = 10, n = 6 のとき 5, m = 10, n = 8 のとき 3 となります。
標準入力から m, n がスペース区切りで与えられるとき、n番目に探索したノードの番号を標準出力に出力してください。
(m, n は m ≧ n を満たす整数とし、m は最大で3000とします)
【入出力サンプル】
標準入力
10 6
標準出力
5
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
class Tree
class Node
attr_accessor :value, :parent, :left, :right
def initialize(value, parent)
@value = value
@parent = parent
@left = nil
@right = nil
end
end
attr_reader :search_count
def initialize()
@root = nil
end
def make!(m)
i = 1
@root = Node.new(i, nil)
queue = [@root]
while !queue.empty?
parent = queue.shift
i += 1
left = Node.new(i, parent)
parent.left = left
if left.value == m then break
else queue << left
end
i += 1
right = Node.new(i, parent)
parent.right = right
if right.value == m then break
else queue << right
end
end
end
def traverse(n)
stack = [@root]
cnt = 0
while !stack.empty?
node = stack.pop
cnt += 1
if cnt == n then return node.value
else
if node.right != nil then stack << node.right end
if node.left != nil then stack << node.left end
end
end
end
end
# main
while line = gets
line.strip!
if line.empty? then next end
m,n = line.split.map{|a| a.to_i}
tree = Tree.new()
tree.make!(m)
p tree.traverse(n)
end
解説
問題の通り、幅優先でツリーを作って、深さ優先で探せばOKです。
考え方
上に書いた通り、幅優先でツリーを作って、深さ優先で探せばOKです。
アルゴリズム的には特に考えるところがないのでコードの説明をみてください。
main
入力値を数値にしてm個の値をもつtreeを作ります。
それをTree#traverse()で探索して結果を印字します。
Treeクラス
treeを管理するクラスで、インスタンスメソッドにmake!()とtraverse()を持ちます。
make!()はツリーを幅優先で構築し、traverse()は深さ優先で探索します。
まぁ、教科書通りの木構造だと思います。
@search_countがありますが消し忘れです。
Tree.Nodeクラス
treeのノードを表す内部クラスです。
メンバ変数には、
@value:ノードの値
@parent:親ノードへの参照(不要だった)
@left:左側の子ノードへの参照
@right:右側の子ノードへの参照
@root:ルートノードへの参照
を持ちます。
Tree.Node#initialize(value, parent)
引数valueはノードの値、parentは親ノードの参照です。
要するに、Nodeのインスタンスを生成すると親ノードと関連づいた子ノードとして生成されるというわけです。
Tree#initialize()
@rootにnilをセットするだけです。
別に要らなかった気がします。
Tree#make!(m)
m個のノードをもつtreeを幅優先で構築します。
@rootを最初に作成します。@rootには親ノードがないのでparentにはnil、valueには1を渡します。
@rootをqueueに入れ、queueから値を1個取り出しては子ノードをつけることを繰り返して行けば幅優先でtreeを構築できます。子ノードは左が小さい値なのでleft、rightの順で子ノードをつけます。同時にカウンタ(i)を加算して、カウンタ(i)がmと同じになったらtreeの構築をやめます。
ちなみにm=10の時、動きは次のようになります。
最初、queueは[1(ノードのvalue)]という状態で、1が取り出されます。
1のleftに2をつけてqueueに入れます。queueは[2]になります。
1のrightに3をつけてqueueに入れます。queueは[2,3]になります。
queueの先頭を取り出すと2なので、2の子に4,5をつけてqueueに入れます。queueは[3,4,5]になります。
queueの先頭を取り出すと3なので、3の子に6,7をつけてqueueに入れます。queueは[4,5,6,7]になります。
queueの先頭を取り出すと4なので、2の子に8,9をつけてqueueに入れます。queueは[5,7,8,9]になります。
queueの先頭を取り出すと5なので、5の子に10をつけて終わります。
紙に書くなどすれば簡単に確認できますが、これできちんと幅優先でtreeができています。
Tree#traverse(n)
深さ優先でn番目に探索したノードの値を返します。
初期値として@rootをstackに入れ、stackから順次値を取り出しながらn回探索した時のノードのvalueを返せば答えになります。
n=6の時の動きは次のようになります。
最初、stackは[1(ノードのvalue)]という状態で、1が取り出されます。探索回数は1なので子ノードを調べます。1の子ノードを見ると2,3なのでstackに積みます。左側を優先するのでright、leftの順でstackに積みます。結果、stackは[3,2]になります。
stackの末尾を取り出すと2です。まだ探索カウントは2なので子ノードを調べ、同様にstackに積みます。2の子は4,5なのでstackは[3,5,4]になります。
stackの末尾を取り出すと4です。まだ探索カウントは3なので子ノードを調べ、同様にstackに積みます。4の子は8,9なのでstackは[3,5,9,8]になります。
stackの末尾を取り出すと8です。まだ探索カウントは4なので子ノードを調べますが子がないのでstackには何も積みません。stackは[3,5,9]になります。
stackの末尾を取り出すと9です。まだ探索カウントは5なので子ノードを調べますが子がないのでstackには何も積みません。stackは[3,5]になります。
stackの末尾を取り出すと5です。探索カウントが6になったので探索をやめ5を返します。
やはりこれも紙に書くなどすればきちんと深さ優先で探索できていることがわかります。
雑感
幅優先探索と深さ優先探索の関係はちょっと面白くて、ループで処理する場合、queueを使うと幅優先に、stackを使うと深さ優先になります。私は昔どこかでこの話を読んだことがあって面白いな、と思っていたのでよく覚えていました。
でも、幅優先探索に比べて深さ優先探索はあまり書いたことがありません。私がやったCodeIQの問題では初めてじゃないかな?
ついでに言うとtreeも自分で実装したことがほとんどありません。treeが必要になるのはデータの検索効率を上げる必要がある場合だと思いますが、C言語以外だとmapとかhashみたいな便利なデータ構造があってそっちを使えば済むことが大半です。ひょっとしたら自力で実装したのは前の会社の新入社員研修以来かも。