CodeIQ：連続する整数の各桁に使われる数字の和

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「連続する整数の各桁に使われる数字の和」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

a, b という2つの正の整数が与えられたとき、aからbまでの連続する整数について、各桁の数字の和を求めることを考えます。

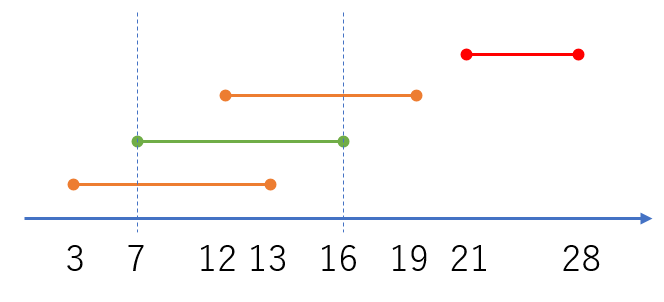
例えば、a = 7, b = 16のとき、7, 8, 9, 10, 11, 12, 13, 14, 15, 16の各桁の数字を足して、
7 + 8 + 9 + 1 + 0 + 1 + 1 + 1 + 2 + 1 + 3 + 1 + 4 + 1 + 5 + 1 + 6 = 52
となります。

また、a = 12, b = 19のときは、
1 + 2 + 1 + 3 + 1 + 4 + 1 + 5 + 1 + 6 + 1 + 7 + 1 + 8 + 1 + 9 = 52
となり、同じ値になります。

このように、同じ値が得られる正の整数 a, b のペアは一つとは限りません。
標準入力から a, b の値がスペースで区切って与えられたとき、与えられた a, b の範囲に重なる（両端を含む）ようなペアがいくつあるかを求め、標準出力に出力してください。
（a = 21, b = 28 なども同じ値になりますが、7～16 と 21～28は重なる範囲がないため対象外です。）

例えば、上記の a = 7, b = 16 の場合、a = 12, b = 19 の他にも a = 3, b = 13 の場合があり、合わせて2通りですので、以下のように出力します。

【入出力サンプル】
標準入力

7 16

標準出力

2
※a, b は32ビット整数の範囲で、0 < b - a < 2500を満たす数が与えられるものとします。

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

# 数字和
def digsum(n)
	n.to_s.split("").reduce(0){|memo, a| memo + a.to_i}
end

# 問題を解く
def solve(a,b)
	cnt = 0

	digsums = {}
	sum = 0
	for n in a..b
		d = digsum(n)
		digsums[n] = d
		sum += d
	end

	# 小さい方
	r = sum - digsums[a]
	s_sum = 0
	smalls = {}
	(a-1).downto(1){|x|
		d = digsum(x)
		s_sum += d
		if s_sum > r then break
		else smalls[s_sum] = x
		end
	}

	s = sum
	(b).downto(a+1){|i|
		s -= digsums[i]
		if smalls[sum-s] != nil then
			cnt += 1
		end
	}

	# 大きい方
	r = sum - digsums[b]
	l_sum = 0
	larges = {}
	(b+1).upto(2*b){|x|
		d = digsum(x)
		l_sum += d
		if l_sum > r then break
		else larges[l_sum] = x
		end
	}

	s = sum
	(a).upto(b-1){|i|
		s -= digsums[i]
		if larges[sum-s] != nil then
			cnt += 1
		end
	}

	return cnt
end

# main
while line = gets
	line.strip!
	if line.empty? then next end

	a, b = line.split.map{|x| x.to_i}
	p solve(a, b)
end

解説

a,bが32bit整数なので計算量を減らす工夫が必要かと思いましたが普通にやって大丈夫でした。

考え方

私の方法は単純です。
例のa=7,b=16の場合で説明します。

まず、a=7,b=16の数字和の合計を計算します。
小さい数字側を探索するために6、5〜6、4〜6、…、1〜6（a-1から1まで）の数字和の合計を計算します。 …… (A)
7〜16の数字和の合計から16の数字和を引いた値を求めます。…… (B1)
(A)の中に(B1)と組み合わせてa=7,b=16の数字和の合計と同じになるものがあるかを探します。
(B1)から15の数字和を引いた値(B2)を求め同じ様にします。これを8（a+1まで）の数字和まで順次繰り返します。
大きい側を探索するために17、17〜18、17〜19、…、17〜32（b+1から2*b）までの数字和の合計を計算します。…… (C)
7〜16の数字和の合計から7の数字和を引いた値を求めます。…… (D1)
(C)の中に(D1)と組み合わせてa=7,b=16の数字和の合計と同じになるものがあるかを探します。
(B1)から7の数字和を引いた値(D2)を求め同じ様にします。これを15（b-1まで）の数字和まで順次繰り返します。

この操作でa=7,b=16の数字和の合計と同じになった物の数が答えになります。

main

入力値からa,bを数値にしてsolve()に渡し、結果を印字します。

digsum(n)

nの数字和を計算します。
nを一旦文字列にして1文字ずつ分解し、各数字を足し合わせています。

solve(a,b)

考え方に書いた通りの実装なので細かい説明は省略し、計算量を減らすための工夫だけを説明します。

まず、a〜bの数字和の合計を求める際に各数字の数字和のリスト（digsums）も作成しています。つまり、a=7,b=16ならdigsums={7=>7, 8=>8, 9=>9, …, 16=>7}という連想配列を作成しています。
こうすることで7〜15、7〜14、…、8〜16、9〜16、…、の数字和の合計を求める時に再度数字和を計算しなくて良い様にしています。

次に、考え方の(B)や(D)を{数字和の合計=>端の値}の形式にしています。例えば小さい側は{6=>6, 11=>5, 15=>4, 18=>3, 20=>2, 21=>1}になります。
こうしておくことで例えば7〜16の数字和の合計52と7〜13の数字和の合計34の差18から3という答えをO(1)で求められます。これはその都度再計算するより早いのはもちろん、配列の中から探すよりもずっと早いです。
そして対応する値がなければnilなのでnilでない場合の回数をカウントすれば答えになるという仕組みです。

雑感

最初、数字和の合計を求めるのに工夫が必要かなと思ってOEISでA037123を調べ、それを利用した実装をしてみたのですが、ローカルで問題の範囲内で最大に近い値を試してみたら遅くてダメでした。
なんとなく、単純にやったほうが早いのでは？と思ってやってみたのが解答のコードです。