CodeIQ：魔方陣で最大値？

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「魔方陣で最大値？」（CodeIQ）を参照してください。

問題の概要

問題を引用します。
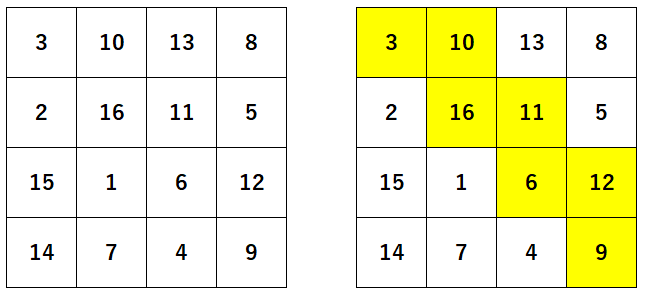
４×４の魔方陣は1～16までの数字を１度ずつ使ったもので、以下の左図のようなものがあります。
魔方陣は縦、横、斜めのすべての列について、その和が等しいという特徴があります。
Fig.1

魔方陣において、左上のマスからスタートして、右か下の隣り合うマスへの移動を繰り返して最短距離で右下のマスまで移動します。
このとき、経由したマスの数の和が最大になるような移動経路を考えます。
上図の魔方陣の場合、上図右のように移動すると和は 67 になります。

標準入力から整数 n が与えられたとき、４×４のすべての魔方陣に対してこのような移動経路を求め、その和が n になる魔方陣の個数を求め、標準出力に出力してください。

４×４の魔方陣は全部で7,040個存在することが知られています。
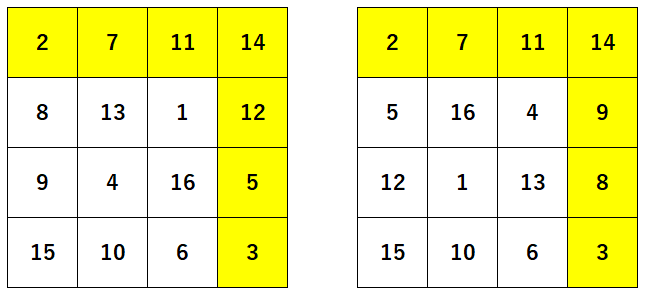
その中で、n=54のときは以下の2パターンに回転や鏡像を含めたものが全部で8通りありますので、以下のような入出力になります。
Fig.2

【入出力サンプル】
標準入力
54

標準出力
8

私のプログラム

Rubyで解答しています。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
#!/usr/bin/ruby
 
def setUsed(used, arr, val)
    for a in arr
        used[a] = val
    end
    return used
end
 
def isDup(x, used, others)
    if used[x] then return true end
    if others.include?(x) then return true end
    return false
end
 
# 次のサイトから移植
# http://www.daido-it.ac.jp/~oishi/TH5/ms4/ms4prg.html
def makeMagicSquare()
    ret = []
    used = Array.new(17,false)
 
    for a in 1..13  # aのループ
        used[a]=true
 
        for d in (a+1)..15  # dのループ
        used[d]=true
 
            for m in (d+1)..16  # mのループ
                q=34-a-d-m                              # qを計算
                if q<a then break end                    # 回転禁止条件より
                if q>16 then next end                    # 16以下であること
                if isDup(q, used, [m]) then next end    # 重複チェック
                used=setUsed(used, [m,q], true)         # 使用済みのフラグを立てる
 
                for f in 1..16  # fのループ
                    if used[f] then next end                # fが既に使用されていないか
                    k=34-a-f-q                              # kを計算
                    if k<1 then break end                    # 1以上であること（kはこの先減る）
                    if k>16 then next end                    # 16以下であること
                    if isDup(k, used, [f]) then next end    # 重複チェック
                    used=setUsed(used, [f,k], true)         # 使用済みのフラグを立てる
 
                    for b in 1..16  # bのループ
                        if used[b] then next end
                        c=34-a-b-d
                        if c<1 then break end
                        if c>16 then next end
                        if isDup(c, used, [b]) then next end
                        used=setUsed(used, [b,c], true)
 
                        for g in 1..16  # gのループ
                            if used[g] then next end
                            j=34-d-g-m
                            if j<1 then break end
                            if j>16 then next end
                            if isDup(j, used, [g]) then next end
 
                            o=34-c-g-k
                            if o<1 then break end
                            if o>16 then next end
                            if isDup(o, used, [j,g]) then next end
 
                            n=34-b-f-j
                            if n>16 then break end
                            if n<1 then next end
                            if isDup(n, used, [j,g,o]) then next end
 
                            used=setUsed(used, [g,j,o,n], true)
 
                            for e in 1..16  # eのループ
                                if used[e] then next end
                                h=34-e-f-g
                                if h<1 then break end
                                if h>16 then next end
                                if isDup(h, used, [e]) then next end
 
                                i=34-a-e-m
                                if i<1 then break end
                                if i>16 then next end
                                if isDup(i, used, [e,h]) then next end
 
                                l=34-d-h-q
                                if l>16 then break end
                                if l<1 then next end
                                if isDup(l, used, [e,h,i]) then next end
 
                                ret << [[a,b,c,d],[e,f,g,h],[i,j,k,l],[m,n,o,q]]
                            end
                            used=setUsed(used, [g,j,o,n], false)     # フラグを降ろす
                        end
                        used=setUsed(used, [b,c], false)     # フラグを降ろす
                    end
                    used=setUsed(used, [f,k], false)     # フラグを降ろす
                end
                used=setUsed(used, [m,q], false)     # フラグを降ろす
            end
            used[d]=false
        end
        used[a]=false
    end
    return ret
end
 
# ダイクストラ法で経路探索
def getMaxPath(map)
    memo = Array.new(4){Array.new(4, 0)}
    directions = [[0,1], [1,0]]
 
    queue = [[0,0]]
    memo[0][0] = map[0][0]
 
    while !queue.empty?
        cur = queue.shift
        v = memo[cur[0]][cur[1]]
 
        for d in directions
            nxt = [cur[0]+d[0], cur[1]+d[1]]
 
            if (nxt[0]<0) || (nxt[1]<0) || (4<=nxt[0]) || (4<=nxt[1]) then next end
            nv = v + map[nxt[0]][nxt[1]]
 
            if nv > memo[nxt[0]][nxt[1]] then
                memo[nxt[0]][nxt[1]] = nv
                queue << nxt
            end
        end
 
        queue.uniq!
    end
 
    return memo[3][3]
end
 
# mapを回転する
def rotateMap(map)
    nxt = Array.new(4){Array.new(4, 0)}
    for i in 0...4
        for j in 0...4
            nxt[j][3-i] = map[i][j]
        end
    end
    return nxt
end
 
# mapを上下鏡像にする
def mirrorMap(map)
    nxt = Array.new(4){Array.new(4, 0)}
    for i in 0...4
        for j in 0...4
            nxt[3-i][j] = map[i][j]
        end
    end
    return nxt
end
 
# 魔方陣の全パターンの最長経路を求める
def makeCountList()
    ret = Hash.new(0)
 
    maps = makeMagicSquare()
    for map in maps
        valiants = [map]
        for _ in 0...3
            valiants << rotateMap(valiants.last)
        end
        valiants << mirrorMap(map)
        for _ in 0...3
            valiants << rotateMap(valiants.last)
        end
 
        for v in valiants
            c = getMaxPath(v)
            ret[c] += 1
        end
    end
 
    return ret
end
 
# main
counts = makeCountList()
while line = gets
    line.strip!
    if line.empty? then next end
 
    p counts[line.to_i]
end

解説

私のプログラムは愚直にやっていますが、もっと効率の良い方法があるのでしょうか？

考え方

考え方は非常に単純で、魔方陣の全てのパターンを求めてからダイクストラ法で経路を計算して入力値の値になるものを数えるだけです。

問題は魔方陣の求め方です。
私はWebで検索して見つけたプログラムをRubyで書き直しただけですが、この方法の考え方は難しくありません。
4隅と中央の4マス、縦横と斜めは合計値が34になるという性質を利用して適当に値を設定し、計算できるところは計算するという方法でやっています。
プログラムの説明の方で詳しくやります。

main

makeCountList()で全ての魔方陣の経路を求め、経路の値毎に何パターンあるかをcountsに保持します。
countsは連想配列なので入力値の値の数を印字します。

makeCountList()

全ての魔方陣の経路を求め、経路の値毎に何パターンあるかを記録した廉造配列を返します。
makeMagicSquare()で回転や鏡像を排除した魔方陣のパターンを生成します。
その1つずつについてrotateMap()で90〜270度回転したもの、鏡像、鏡像を90〜270度回転したものを生成し、その全てについてgetMaxCount()で経路の値を求めます。
経路の値をキーとし、その値になる経路の数を廉造配列に記録し、返却します。

makeMagicSquare()

回転や鏡像を排除した魔方陣の全パターンを作成します。
やり方は次の通りです。

次のような図を考えます（記号はプログラムと合わせています）。
abcd
efgh
ijkl
mnoq

a,d,mの値を適当に決めます（値の重複がないように任意の値を選ぶ）。
この3箇所が決まるとqが決まります。
この時a<d<m、q<aとすることで回転と鏡像を排除します。
a bc d
efgh
ijkl
m no q

次にfを適当に決めます。
するとkが決まります。
a bc d
e f gh
ij k l
m no q

次にbを適当に決めます。
するとcが決まります。
a b c d
e f gh
ij k l
m no q

次にgを適当に決めます。
するとj,oが決まり、jかoが決まるとnが決まります。
a b c d
e f g h
i j k l
m n o q

最後にeを適当に決めます。
するとh,iが決まり、hかiが決まるとlが決まります。
a b c d
e f g h
i j k l
m n o q

プログラム中ではa〜qの変数で各マスの値、usedですでに使用済みの値を管理しています。候補値が確定する毎にusedの添え字番号の値をtrueにし、ループを抜ける毎に当該箇所をfalseに戻します。
setUsed()はusedの添え字番号に一致する値をtrueかfalseにセットする関数です。
isDup()は重複チェックを行う関数で、xが候補値、usedが使用済みの値管理テーブル、othersはusedに記録されていないけれど、計算などで求まった候補値です。
この2つの関数は単純なので解説しません。

rotateMap(map)、mirrorMap(map)

rotateMap()は2次元配列を90度回転したものに、mirrorMap()は上下方向の鏡像に変換します。いずれも単純な座標の入れ替えなのでコードを見てください。

getMaxPath(map)

引数mapに基づいて問題通りに最大の値になる経路を探索します。
ダイクストラ法で右か下方向に値を辿り、そのマスに到達した時に最も大きな値になるものだけを保持して、最終的に右下の値を返すだけです。

雑感

私のやり方は完全な総当たりですがもっと効率の良い方法がある気はします。
その上、魔方陣を解く関数のネストがヒドく、ちょっとどうかと思います（人のコードを移植しておいてアレですが）。
私は魔方陣を回転、鏡像を除いて列挙した上で回転、鏡像を作成しています。多分、一気に全て列挙するよりもこちらの方が速いと思うのですがどうでしょう？