CodeIQ:放物線とマス目の関係
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「放物線とマス目の関係」(CodeIQ)を参照してください。
問題の概要
【概要】
放物線の方程式とマス目を指定するので、位置関係がどうなっているのかを計算してください。
【詳細】
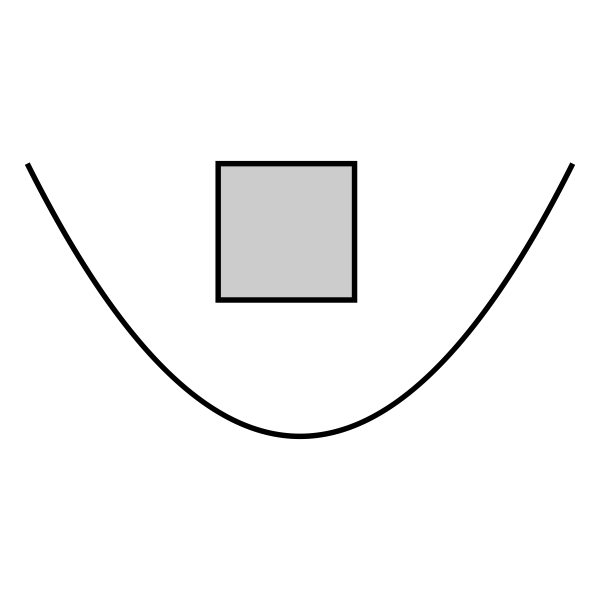
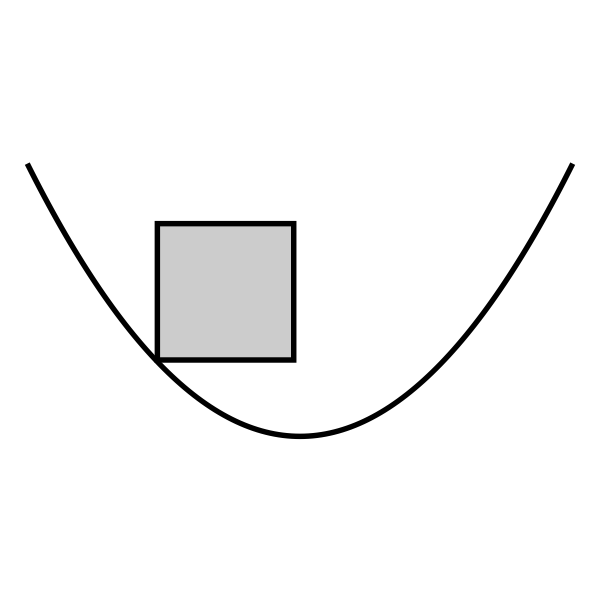
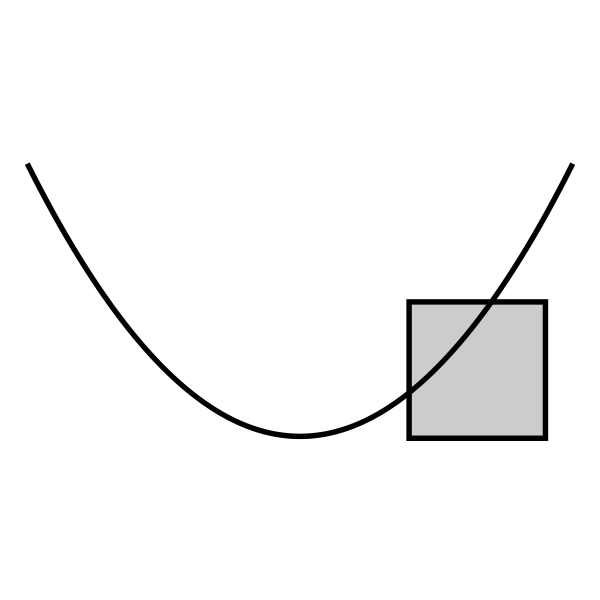
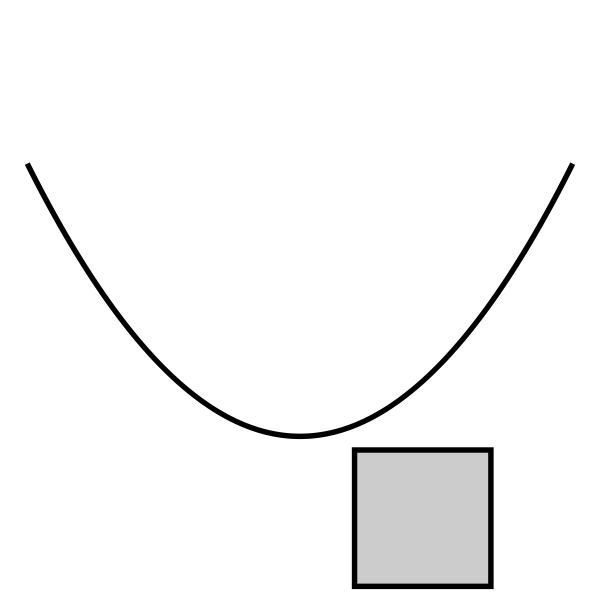
放物線とマス目の位置関係は下表の5種類があります(以下、y 座標が大きい方向が上、x座標が大きい方向が右、になります):
記号 状況 例 U 完全に放物線より上にある u マス目の内部は放物線より上にあるが、マス目と放物線に共有点がある。 S マス目を放物線が分断し、放物線より上にも下にも 0 より大きな面積がある L 完全に放物線より下にある l マス目の内部は放物線より下にあるが、マス目と放物線に共有点がある。
【入出力】
入力は
1 0 0 0 -3
のようになっています。
空白区切りになっていて、順に a, b, c, X, Y です。
a, b, c は、放物線
y=ax2+bx+c
の係数です。
X, Y はマス目の左下隅の座標です。マス目の大きさは、 1×1 です。
つまり、マス目の領域は
(x,y) = { |x,y| X≦x≦X+1, Y≦y≦Y+1 }
です。
出力は、
L
のような感じです。
U,u,S,L,lのいずれかを出力してください。
【例】
入力 出力 1 0 0 0 -3 L 1 0 -46 7 4 S
【補足】
不正な入力に対処する必要はありません。
a は、-100000 以上 100000 以下のゼロではない整数です。
b, c, X, Y は、-100000 以上 100000 以下の整数です。
分断される場合に出力されるSは、大文字です。ご注意ください。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 放物線の頂点の座標
def getPeakPos(a, b, c)
x = -1*Rational(b, 2*a)
y = a * (x**2) + b * x + c
return [x, y]
end
# 放物線の頂点が四角形の内側にあるかを調べる
def isPeakInSquare(peak, x, y)
if (x < peak[0]) && (peak[0] < x+1) && (y < peak[1]) && (peak[1] < y+1) then
return true
else
return false
end
end
# 四角形の角座標が放物線の上にあれば+1、下にあれば-1、同じなら0を返す
def checkPosition(a,b,c,x,ys)
yp = a * (x**2) + b * x + c
if ys-yp < 0 then return -1
elsif ys-yp > 0 then return +1
else return 0
end
end
# 放物線の上、下、線上にある点の数を数える
def countPointsPos(pos)
ret = [0,0,0] # 放物線の上、放物線の下、放物線上
for v in pos
if v > 0 then ret[0] += 1
elsif v < 0 then ret[1] += 1
else ret[2] += 1
end
end
return ret
end
def solve(a,b,c,x,y)
peak = getPeakPos(a, b, c)
# 放物線の頂点が四角形の内側にある場合は必ず"S"になる
if isPeakInSquare(peak, x, y) then return "S" end
# 放物線の頂点がX軸に平行な線分上にある場合
if peak[1] == y+1 then # 上の線と接している
if a > 0 then # 凹側
return "l"
elsif a < 0 then # 凸型
return "S"
end
elsif peak[1] == y then # 下の線と接している
if a > 0 then # 凹側
return "S"
elsif a < 0 then # 凸型
return "l"
end
end
points = [[0,0], [1,0], [0,1], [1,1]] # 左下、右下、左上、右上
pos = []
for point in points
pos << checkPosition(a, b, c, x+point[0], y+point[1])
end
cnt = countPointsPos(pos)
if (cnt[0] > 0) && (cnt[1] > 0) then # 放物線より上と下の点が1以上ある = 放物線と四角形が交わっている
return "S"
elsif (cnt[0] > 0) && (cnt[1] == 0) && (cnt[2] == 0) then # 放物線より上の点しかない
# 放物線の頂点が四角形のX座標の間で下の線よりも上にある
if ((x < peak[0]) && (peak[0] < x+1)) && (peak[1] > y+1) then
return "S"
else
return "U"
end
elsif (cnt[0] == 0) && (cnt[1] > 0) && (cnt[2] == 0) then # 放物線より下の点しかない
# 放物線の頂点が四角形のX座標の間で下の線よりも下にある
if ((x < peak[0]) && (peak[0] < x+1)) && (peak[1] < y) then
return "S"
else
return "L"
end
elsif (cnt[0] > 0) && (cnt[1] == 0) && (cnt[2] > 0) then # 放物線より上の点と接点がある
return "u"
elsif (cnt[0] == 0) && (cnt[1] > 0) && (cnt[2] > 0) then # 放物線より下の点と接点がある
return "l"
end
return "?"
end
# main
while line = gets
line.strip!
if line.empty? then next end
a, b, c, x, y = line.split.map{|v| v.to_i}
puts solve(a,b,c,x,y)
end
解説
ぱっと見は難しそうではなかったのですが、意外と苦労しました。
その上、私のコードには正しく判定できない場合がありそうな気がしています。
考え方
- 放物線の頂点が四角形の内側にあるなら必ず"S"
- 四角形の角の座標のうち、4つともが放物線の下にあれば"L"
- 四角形の角の座標のうち、4つともが放物線の上にあれば"U"
- 四角形の角の座標のうち、1つが放物線上にあり、残りが放物線の下にあれば"l"
- 四角形の角の座標のうち、1つが放物線上にあり、残りが放物線の上にあれば"u"
- 放物線の上と下の両方に点があれば"S"
これだけでは漏れがあって、次のパターンを正しく判定できません。
- 放物線が四角形を突き抜いている場合(四角形の角は全て放物線の上(凸型の場合)か下になる(凹型の場合))
- 凹型の放物線が四角形の上辺に接している場合(四角形の角は全て放物線の下)
- 凸型の放物線が四角形の下辺に接している場合(四角形の角は全て放物線の上)
接している方は簡単に判断できます。
放物線の頂点のx座標は-a/2bなのでそこからy座標を計算し、四角形の座標と比較すれば良いわけです。
放物線が四角形を突き抜いている場合ですが、これは私の実装で十分か自信がありません。
私がやったのは、放物線の頂点が四角形の角のx座標の間にあって、頂点が四角形より下、四角形の角が全て放物線より下なら突き抜いている、です(凹型の場合。凸型なら反対になります)。
一応、以上の処理を実装したらテストケースをパスしました。
main
入力値を solve()に渡します。
solve()が結果を返すのでそれを印字して終わります。
solve(a,b,c,x,y)
答えを計算します。
まず、放物線の頂点が四角形の内側(線上は含まない)にあるかを調べ、四角形の内側にあれば"S"を返却して終わります。
次に放物線と四角形の上下の線が接しているかをチェックします。凹型の場合、上の線に接していると"l"、下の線に接していると"S"で、凸型なら上の線に接していると"S"、下の線に接していると"l"ですからこれを返却して終わります。
そして次のように判定して結果を返します。
- 放物線の上と下の両方に点があれば"S"
- 四角形の角の座標のうち、4つともが放物線の上にある
- 放物線の頂点が四角形のX座標の間で上の線よりも上にあるなら"S"
- それ以外は"U"
- 四角形の角の座標のうち、4つともが放物線の下にある
- 放物線の頂点が四角形のX座標の間で下の線よりも下にあるなら"S"
- それ以外は"L"
- 四角形の角の座標のうち、1つが放物線上にあり、残りが放物線の下にあれば"l"
- 四角形の角の座標のうち、1つが放物線上にあり、残りが放物線の上にあれば"u"
getPeakPos(a, b, c)
放物線の頂点座標を計算します。
浮動小数点が嫌なのでRationalを使います。
isPeakInSquare(peak, x, y)
放物線の頂点が四角形の内側にあるかを調べます。
peakが放物線の頂点、xとyは入力値です。
単純にx < peak[0] < x+1かつy < peak[1] < y+1なら内側に頂点があり、そうでなければ無いと判断します。
checkPosition(a,b,c,x,ys)
四角形の角が放物線に対して上、下、線上のどれかを計算します。上なら1、下なら-1、線上なら0を返します。
x座標を放物線の式に当てはめれば放物線のy座標がわかるので、それと入力値から求めた四角形の角のy座標を比較するだけです。
countPointsPos(pos)
放物線に対して四角形の角[左下,右下,左上,右上]が上、下、線上のいずれにあるかがわかっているとして、それを[上にある数、下にある数、線上にある数]の配列に変換します。
雑感
最初、線上で接しているパターンや突き抜いているパターンを考えていなくてリジェクトされました。デバッグにはMacのグラフ計算機が非常に役に立ってくれました。
実のところ、放物線に対して上、下、線上にある四角形の角の数(これは実装している通り)と、四角形の4辺に対して放物線が交わっているかどうかの情報を使えば自信がないなどということはなく、正しく判定できると思うのです。ただ、こちらは四角形のx軸に平行な辺と放物線の交点の有無を調べる時に浮動小数点を使わざるをえない(と思う)ので採用しませんでした。浮動小数点を使わずに交点の有無をうまく判断できる方法があるのでしょうか?