CodeIQ:スパイラル・ウォーク
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「スパイラル・ウォーク」(CodeIQ)を参照してください。
問題の概要
自然数 w, h に対し、横と縦の長さがそれぞれ w, h となる格子状の道を考えます。
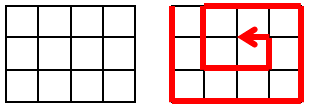
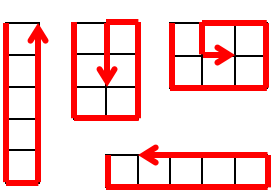
この左上の点からスタートして、同じ交差点を二度以上通らないように、らせんを描いて進みます。
最初は下方向にまっすぐ進み、これ以上前に進めなくなったところで左折し、再びまっすぐ進みます。
これを繰り返し、全ての交差点に到達したところで終了します。
(w, h)=(4, 3) の場合の進み方を下に示します。このとき進んだ距離は 19 であることが分かります。
自然数 m に対し、上のように進んだ時の距離がちょうど m となるような組 (w, h) の個数を F(m) と定義します。
例えば F(11)=4 です。進んだ距離が 11 となる組 (w, h) は、(1, 5), (2, 3), (3, 2), (5, 1) の 4 通りです。
同様に、F(3)=1, F(23)=6, F(28)=0 となることが確かめられます。
さらに、自然数 n に対し、1≦m≦n となる全ての m に対する F(m) の和を G(n) と定義します。
例えば、G(11)=12, G(100)=283, G(1000)=5076 となることが確かめられます。
標準入力から、自然数 n(1 ≦ n ≦ 106)が与えられます。
標準出力に G(n) を出力するプログラムを書いてください。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby def A006218(n) s = 0 for i in 1..Math.sqrt(n).floor s += n / i end return 2*s-Math.sqrt(n).floor**2 end def G(n) if n < 4 then return 0 end ret = A006218(n) ret -= 5 # n=0..3の分を引く ret -= 2*(n-3) # n>=4においてはnの約数の個数-2が答えを求めるために必要 return ret end # main while line = gets line.strip! if line.empty? then next end p G(line.to_i+1) end
解説
nの最大が1000000もあることを除けば難しくありません。
nが1000000もあることに対応するのが超難しい(私の数学能力では自力では無理)です。
考え方
F(n)は簡単にわかります。
問題文では(w,h)を線の数としていますが、(w',h')を上辺と左辺上の格子点の数とすると
m=w'*h'-1
になることはすぐわかります。
ということはF(n)はm+1をa*bという2数の積の形で表せるパターン数-2になります。
-2は1*b、a*1の形が成立しないためです。
また、格子点の数が4未満の図形は作れないのでその点は考慮する必要があります。
後は入力値n+1までF(n)を足し合わせれば良いのですが、nは最大1000000なので全然間に合いません。なのでn+1以下の全ての数の2数の積の形で表せるパターン数の合計を計算だけで求める方法が必要です。
わからないのでいつものようにOEISで調べたらA006218があったので、その中でわかりやすく速そうな式を利用しました。式は
a(n) = 2*(Sum_{i=1..floor(sqrt(n))} floor(n/i)) - floor(sqrt(n))^2. - Benoit Cloitre, May 12 2002
です。
計算量がO(√n)なのでn=1000000なら十分です。
main
入力値を数値に変換し、入力値+1を G()に渡します。
G()が結果を返すのでそれを印字して終わります。
G(n)
答えを計算します。
A006218(n)はn以下の数の2数の積の形のパターン数の合計を返します。
15行目で5を引いているのはn=1..3(コメントが間違っています)の場合、そのような図形は成立しないのでそのパターン数を無視する必要があるためです。n=1は(1,1)、n=2は(1,2)、(2,1)、n=3は(1,3)、(3,1)で合計5パターンという訳です。
16行目はn≧4に置いて(1,b)、(a,1)のパターンは図形として成立しないのでそのパターン数を減らす必要があるためです。
結果の数を返却します。
A006218(arr)
OEISで調べた式をコード化しただけです。
雑感
考え方に書いたことは割とすぐにわかったのですが、A006218にたどり着くのに苦労しました。
というか、メモ化とか動的計画法でうまく高速化できるんでしょうか?