CodeIQ:交互に取り合うカード
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「交互に取り合うカード」(CodeIQ)を参照してください。
問題の概要
m 枚のカードがあります。
2人がカードの中から何枚かを取ることを交互に繰り返します。
最後のカードを取った人の合計枚数が多い場合、最後に取った人の勝ちとします。
(最後に取れなかった人は負け、最後に取っても合計枚数が同じか少ないと負けになります。)
一度に取ることができる枚数には上限 n があり、1~n 枚の中から任意の枚数を取ります。
このとき、先手が勝つような取り方が何通りあるかを求めてください。
なお、双方とも少なくとも1枚は毎回必ず取るものとします。
例えば、m = 6, n = 1のときは、1枚ずつ取ることになるため、先手が勝つことはできません。
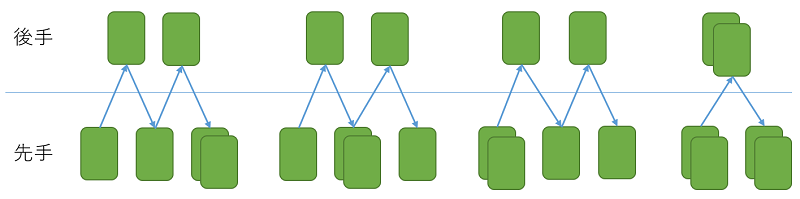
m = 6, n = 2のときは、以下の4通りがあります。
整数 m, n がスペースで区切って標準入力から与えられるとき、先手が勝つパターンが何通りあるかを求め、標準出力に出力してください。
入力の m, n の範囲は、出力されるパターン数が32bit整数に収まるように与えられるものとします。
【入出力サンプル】
標準入力
6 2
標準出力
4
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def getNext(before, m, n, t)
results = {}
wins = 0
before.each{|ptn, cnt|
for i in 1..n
if t == 0 then
nxt_p = [ptn[0]+i, ptn[1]]
else
nxt_p = [ptn[0], ptn[1]+i]
end
if nxt_p[0] + nxt_p[1] > m then break
elsif nxt_p[0] + nxt_p[1] == m then
if (t == 0) && (nxt_p[0] > nxt_p[1]) then wins += cnt end
else
if results[nxt_p] == nil then
results[nxt_p] = cnt
else
results[nxt_p] += cnt
end
end
end
}
return results, wins
end
def solve(m,n)
results = {[0,0]=>1}
count = 0
t = 0
while !results.empty?
results, c = getNext(results, m, n, t%2)
count += c
t += 1
end
return count
end
# main
while line = gets
line.strip!
if line.empty? then next end
m,n = line.split.map{|a| a.to_i}
p solve(m,n)
end
解説
★★★の問題でしたがそれほど難しくないと感じました。というか、同じ出題者によるここ10回くらいの中では一番簡単だったように思えます。
考え方
ポイントは答えが32bit整数以下なので、答えに含まれないものも考慮すると非常にパターン数が多いという1点だけです。
まず、基本的には動的計画法でできそうです。
先手が1〜n枚カードを取り、そのすべてのパターンに対して後手が1〜n枚カードを取り、…、というのを繰り返してすべてのパターンを列挙することができます。先手、後手の合計枚数がm以上になったらそのパターンにカードを追加するのをやめて、カードを撮るのをやめた時に手番でなかったら負けにするのは問題の通りに実装すれば良いでしょう。
問題は、この通りにパターンを列挙しているとパターン数が多すぎて制限時間内に終わらないことです。なので、処理するパターン数を減らす工夫が必要です。
例えば先手が1,3、後手が2,3とカードをとった場合も、先手が2,2、後手が1,4とカードをとった場合も先手4枚、後手5枚であることには変わりありません。5回目にカードをとる場合は、この先手4枚、後手5枚に対して1〜n枚のカードを追加することを考えれば良いのです。
なので、x回目にカードを時を考えると1〜x-1回目にどのようなパターンでカードをとったかは関係なく、現在何枚のカードを持っているのかだけが重要なことがわかります。
従って、[先手枚数,後手枚数]=パターン数という情報を管理することで計算すべきパターン数を大幅に減らすことができます。
main
入力値を数値に変換し、solve()に渡します。
solve()が結果を返すのでそれを印字して終わります。
solve(m,n)
引数は入力値です。
resultsは先手、後手、先手、…、の順番でカードをとった場合、それぞれの手番が終わった時のまだ決着がついていない[先手,後手]のカード枚数をキー、その枚数になるパターン数を値とする連想配列です。初期値はそれぞれ0枚ずつを持っているパターンが1パターンだけなのでそれを設定しておきます。
countは答えのパターン数です。
tは先手か後手のどちらの手番かを管理するためのパラメータで、手番ごとに1,2,3,…、と単純に1ずつカウントアップします。
36〜40行目のwhileループで手番ごとのパターンを作ります。実際の処理はgetNext()が行うので、結果を受け取るだけです。
getNext()は決着がついていないパターンと先手勝ちになったパターン数を返します。決着がついていないパターンでresultsを更新し、先手勝ちになったパターンはcountに加算します。
tは1回ごとにカウントアップします。
すべてのパターンに決着がついた=残りカード枚数が0になった場合、resultsの要素数は0になるのでwhileループが終了します。
ループが終了した時のcountが先手勝ちのパターン総数なのでこれを返します。
getNext(before, m, n, t)
引数beforeは前回の[先手,後手]のカード枚数とそのパターン数を記録した連想配列です。
m,nは入力値です。
tは先手か後手どちらの手番かを表し、0は先手、1は後手になります。
変数resultsは前回のパターンに今回の手番でのカードを追加したパターンを保持する領域、winsは先手勝ちになったパターン数です。
7〜26行目のループで前回のパターンすべてに対して処理を行います。
8〜25行目のループで1〜n枚のカードを追加します。9〜13行目は今回の手番のプレイヤーにカードを追加する処理です。
先手、後手のカード枚数合計がmを超えたら、それ以上カードを取れないのでループをブレークします(15行目)。
先手、後手のカード枚数合計がちょうどmなら勝ち負けが決まります(16行目)。先手の手番で先手の枚数>後手の枚数なら先手勝ちなのでwinsにパターン数を加算します(17行目)。
それ以外(カード枚数の合計がm未満)の場合は次の手番になるので、前回のパターン数から今回のカードを加えたパターン数を求めます(18〜23行目)。
ループを抜けたらresultsとwinsを返します。
雑感
この出題者の問題では久しぶりにチャチャっと終わりました。前にも同じようなプログラムを書いた記憶があるのでそのせいもあると思います。
連想配列(JavaやC++のMapでも)を使える言語なら同じようにできますが、C言語だとどうするかなぁと考えてみました。面倒かと思ったのですが、2次元配列で表現できるのでそうでもなさそうです。