CodeIQ:迷路の最長経路
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「迷路の最長経路」(CodeIQ)を参照してください。
問題の概要
横に w マス、縦に h マス並んでいるマスのいくつかを塗りつぶして、迷路を作ります。
塗りつぶしたところが壁になり、塗りつぶされていないところが通路になります。
スタートが左上のマス、ゴールが右下のマスである迷路を一度に1マスずつ「右手法」で進みます。
右手法は、右側の壁を触りながら壁沿いに進む方法で、最短経路が求められるとは限りませんが、最終的にスタートに戻るかゴールに到達します。
n マスを塗りつぶすとき、スタートからゴールまでに経由するマスを数えます。
なお、ゴールに到達できないような迷路は考えないものとします。
同じマスを複数回通った場合は別々にカウントし、ゴールのマスに到達した時点で終了とします。
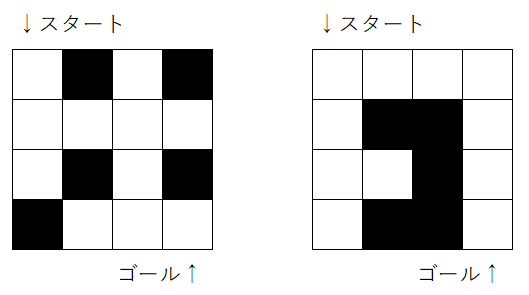
例えば、w = 4, h = 4, n = 5 のとき、左図のような場合は「↓↓↑→→↓↓←→→」のように移動しますので、11マスになります。
標準入力から w, h, n がスペース区切りで与えられたとき、経由するマスが最長になるような塗りつぶすマスの配置を求め、その経由するマスの数を標準出力に出力してください。
例えば、w = 4, h = 4, n = 5 のとき、最長になるのは上の右図のようなパターンがありますので、「15」を出力します。
なお、経由するマスは最大でも25になるような w, h, n が与えられます。
【入出力サンプル】
標準入力
4 4 5
標準出力
15
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 壁かどうかをチェックする
def isWall(pos, dir, wall, w, h)
np = [pos[0]+dir[0], pos[1]+dir[1]]
bnp = (1 << (np[0]*w+np[1]))
if np[0] < 0 || np[0] >= h || np[1] < 0 || np[1] >= w then
return true
end
return (wall & bnp) == bnp
end
# 右手法で迷路を探索する
# 1. 進行方向の右側が通れるなら右に回る
# 2. 右に曲がれないならまっすぐ進む
# 3. まっすぐ進めないなら左に進む
# 4. 3方向ともダメならUターンする
def walk(wall, pos, dir, w, h)
right = {
[1,0] => [0,-1],
[-1,0] => [0,1],
[0,1] => [1,0],
[0,-1] => [-1,0],
}
left = {
[1,0] => [0,1],
[-1,0] => [0,-1],
[0,1] => [-1,0],
[0,-1] => [1,0],
}
u_turn = {
[1,0] => [-1,0],
[-1,0] => [1,0],
[0,1] => [0,-1],
[0,-1] => [0,1],
}
# 探索順(右、前、左、後ろ)
dirs = [right[dir], dir, left[dir], u_turn[dir]]
dirs.each{|nd|
np = [pos[0]+nd[0], pos[1]+nd[1]]
bnp = (1 << (np[0]*w+np[1]))
if np[0] < 0 || np[0] >= h || np[1] < 0 || np[1] >= w then
next
elsif (wall & bnp) == bnp then
next
else
# 現在位置から見て次の進行方向の左右後が壁なら二度と通る必要がないので壁にする
nwall = wall
r = isWall(pos, right[nd], nwall, w, h)
l = isWall(pos, left[nd], nwall, w, h)
b = isWall(pos, u_turn[nd], nwall, w, h)
if r && l && b then nwall |= (1 << (pos[0]*w+pos[1])) end
return [np, nd, nwall]
end
}
return [nil, nil, wall]
end
# 現在の壁の配置でのマス数を数える
def getPathCount(wall, w, h)
st = [0,0]
gl = [h-1,w-1]
cnt = 1
pos = st
dir = [1,0]
nwall = wall
while true
pos, dir, nwall = walk(nwall, pos, dir, w, h)
if pos == nil then return 0
elsif pos == gl then break
else cnt+=1
end
if cnt > 25 then return 0 end
end
return cnt+1
end
# 問題を解く
def solve(w, h , n)
ret = 0
queue = [0]
# 壁を1つずつ増やす
for _ in 1..n
ret = 0
nqueue = []
# 一つ前の最澄経路の壁パターン全てに対して新規に壁を追加
for q in queue
# スタートとゴールを除く全部のマスをチェック
for i in 1...(w*h-1)
# ビットパターンにしてすでに壁のある場所は無視
nw = 1 << i
if (q & nw) == nw then next end
wall = q | nw
cnt = getPathCount(wall, w, h)
if cnt > ret then
nqueue = []
nqueue << wall
ret = cnt
elsif cnt == ret then
nqueue << wall
end
end
end
queue = nqueue
end
return ret
end
# main
while line = gets
line.strip!
if line.empty? then next end
w, h, n = line.split.map{|a| a.to_i}
p solve(w,h,n)
end
解説
★★★の問題です。解いてしまった後ではそれほどでも無いように思えますが、やっている時は非常に難しいと思いました。というか、問題を一読した時点ではギブアップの可能性も濃厚だと感じたほどです。
ポイントは2点あって1つは右手法での迷路探索、もう一つは計算量です。
右手法の迷路探索はやればできます。問題は計算量の方で、すべての壁の配置に対して右手法で探索するのは大変なことになってしまいます。
考え方
マップのサイズ(w,h)に関する言及はありませんが最も長い経路で25なのでそれほど広くはなさそうです。壁の配置はw*hCn通りになりますが、w*h=30くらいですでに辛そうです。
結論としては任意の場所に壁を1つ配置し、最長経路となるパターンを残す。そのパターンに対して重複しない場所に壁を配置し、最長経路となるパターンを残す。これを壁がnになるまで繰り返すことで答えを求められます。
この方法だと最長経路となるすべてのパターンはわかりません。1回目の壁はマップの左端の列か一番下の行に配置されるからです。ですが、最長経路のパターンを全て求める必要はなく、何マス必要かだけわかれば良い(=1パターンでもこの方法で見つけられれば良い)ので、これで答えを求められます。
- 進行方向の右側が通れるなら右に回る
- 右に曲がれないならまっすぐ進む
- まっすぐ進めないなら左に進む
- 3方向ともダメならUターンする
- ゴールにたどり着くまで1〜4を繰り返す
main
入力値を数値に変換しsolve()に渡します。
solve()が結果文字列を返すのでそれを印字して終わります。
solve(w, h, n)
引数はそれぞれ入力値です。
retは答えのマス数です。
queueは壁の数が1〜nまでの各段階の最長経路を保持する領域です。
まず、壁の数を1〜nまで処理を繰り返します(100〜126行目)。
壁の数が増えるごとにretは0にリセットします(101行目)。
nqueueは各段階の壁の数での最長経路になる壁の位置パターンの配列です。
queueからパターンを1つ取り出し(105〜122行目)、スタートとゴール以外の全ての箇所に壁を配置します(107〜121行目)。私のプログラムは壁の位置をビットパターンとして保持しているので1以上(w*h−1)未満がスタートとゴール以外の場所になります。
新たな壁をビットパターンにし(109行目)、すでに現在のパターンのその位置に壁があれば無視します(110行目)。そうでなければパターンに新しい壁を追加します(112行目)。
getPathCount()でその壁の配置でのスタートからゴールまでマス数を右手法で数えます。
結果がretより大きければnqueueを新規作成し、そのパターンを追加し、retを更新します。retと同じならqueueに壁のパターンを追加します。
全てのパターンをこなしたらqueueをnqueueで更新し、壁を増やして上記の処理を繰り返します。
最終的にループが終わった時のretが答えになるので、これを返します。
getPathCount(wall, w, h)
引数wallは壁の配置(ビットパターン)、w、hは入力値です。
stはスタート座標、glはゴール座標です。
cntはスタートからゴールまでのマス数です。
posは現在位置、dirは進行方向です。
nwallはwalk()の処理に関係があって用意した変数です。walk()は渡された現在位置が3方向壁に囲まれていたらその場所を壁に更新します(同じ場所の行ったり来たりを回避するため)。なので更新された壁の位置を保持する領域としてnwallを使用します。
探索は無限ループ(80〜89行目)でwalk()を呼び出し、座標、進行方向、更新された壁の位置を戻り値として得ます。
posがゴールならループを抜け(84行目)、そうでなければcntを1増やしてループを繰り返します(85行目)。また、walk()は進む場所がなければnilを返すのでnilが返った場合は0をリターンします。
88行目は念のための終了条件です。
ループを抜けた時のcntにゴールの場所の1を加えた値が経路のマス数なのでそれを返します。
walk(wall, pos, dir, w, h)
引数wallの壁の配置に対し、posの座標から進める方向に進み、次の位置、方向、更新した壁の配置、を返します。引数dirは現在の進行方向です。これは右手法が現在の進行方向に対して右を基準にするので必要になります。wとhは入力値です。
right、left、u_turnは現在の進行方向に対して右、左、反転方向を返すための定数です。
dirsは右手法の優先順位に従って進行方向を列挙したもので、現在の進行方向を基準に右、前、左、後ろの順で方向を列挙しておきます(43行目)。
dirsの順に進行方向を取り出して、その方向に進めるかをチェックします(45〜45行目)。
npは次の座標(47行目)で、nbpはそれをビット表現にしたものです。
座標が範囲外なら進めないので無視します(50〜51行目)。
座標が壁の場所ならやはり進めないので無視します(52〜53行目)。
それ以外なら次の座標、進行方向、壁の配置を返します(63行目)。壁の配置ですが、現在の進行方向を基準に右左後が壁なら引数に渡された現在位置(pos)を壁にします(56〜61行目)。これによって2回以上通る必要のない場所を通らなくてよくなります。
ループを抜けた場合、進める場所がなかったので次の位置、進行方向をnilにして返します(67行目)。
isWall(pos, dir, wall, w, h)
引数posに渡された座標から見て、wallの壁の配置で、dirの方向が壁かどうかをチェックします。wとhは入力値です。
範囲外とwallに含まれる座標だったら壁なのでtrue、そうでなければfalseを返します。
雑感
最初に書いた通り、かなり苦労しました。
最初思いついたのは壁が渦巻状になっているパターンが最長経路ではないかと思ったのですが、これは間違っていました。仕方ないので、総当たりでやってみることにしました。これはリジェクトされた時にテストケースが判明していて総当たりでも行けるのでは? という感じだったからです。が、時間オーバーは明らかでした。
仕方ないので最長経路になるパターンを印字して眺めていたら、少なくとも1パターンでも見つけられれば答えになるのでは? と気づいて今回のプログラムになりました。