CodeIQ:公平に分けられたケーキ2
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「公平に分けられたケーキ2」(CodeIQ)を参照してください。
問題の概要
ケーキを公平に分けるとき、太郎と次郎の2人がいる場合は以下の方法が有名です。
太郎がケーキを自分の価値観で公平であるように2つに分ける。
次郎が好きな方を選び、太郎は残りを取る。
今回は、太郎、次郎、三郎、…、m 郎の m 人で公平に切り分けることを考えます。
横幅が n の長方形のケーキを左から順に各自の価値観で垂直に切り、最後の人から逆順に好きな部分を選ぶものとします。
切ったケーキの横幅はいずれも整数になるものとします。
このとき、最大のケーキと最小のケーキの横幅の差が w 以下となるような切り方が何通りあるかを求めてください。
なお、ケーキを切らない選択も可能とします。
また、途中でケーキの幅が狭くなり切れなくなった場合は、そこで切るのをやめます。
最後の人から順に選ぶため、前半に切った人はケーキが割り当てられない場合があります。
このとき、ケーキの幅は 0 です。
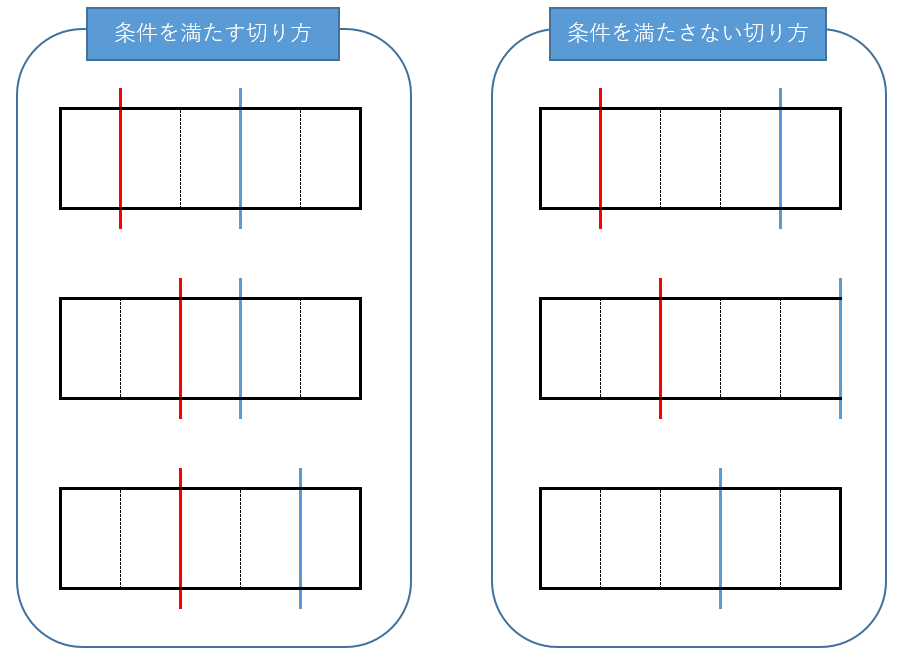
例えば、m = 3, n = 5, w = 1 のとき、以下の図の左側にある3通りが考えられます。
右側のようなパターンは条件を満たさないため、不適切です。
標準入力から正の整数 m, n, w がスペースで区切って与えられます。 上記の条件を満たす切り方が何通りあるかを求め、標準出力に出力してください。
なお、m < n < 40, w < 10 とします。
【入出力サンプル】
標準入力
3 5 1
標準出力
3
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 2〜m-1回の分割を処理する
def getNext(pattern, n, w)
ret = Hash.new(0)
pattern.each{|ptn, cnt|
st = (ptn["mn"]-w > 0) ? ptn["mn"]-w : 0
ed = ptn["mn"]+w
for i in st..ed
mn = (i < ptn["mn"] ? i : ptn["mn"])
mx = (i > ptn["mx"] ? i : ptn["mx"])
sum = ptn["sum"] + i
if (sum <= n) && (mx-mn <= w) then
nkey = {"mx"=>mx, "mn"=>mn, "sum"=>sum}
ncnt = ret[nkey] + cnt
ret[nkey] = ncnt
end
end
}
return ret
end
# m回目の分割を処理する
def getLast(pattern, n, w)
# puts "----- last -----" # DEBUG
ret = Hash.new(0)
count = 0
pattern.each{|ptn, cnt|
# printf("%s : %d\n", ptn.to_s, cnt) # DEBUG
l = n - ptn["sum"] # 最後に残ったケーキの大きさ
mn = l < ptn["mn"] ? l : ptn["mn"]
mx = l > ptn["mx"] ? l : ptn["mx"]
sum = ptn["sum"] + l
# printf("mx=%d, mn=%d, sum=%d, cnt=%d, l=%d\n", mx, mn, sum, cnt, l) # DEBUG
if (mx-mn) <= w then
nkey = {"mx"=>mx, "mn"=>mn, "sum"=>sum}
ncnt = ret[nkey] + cnt
# printf("%s : %d\n", nkey.to_s, cnt) # DEBUG
ret[nkey] = ncnt
count += cnt
end
}
# p ret # DEBUG
return count
end
def init(m,n,w)
ret = {}
mn = ((n-(m-1)*w).to_f / m).ceil
if mn < 0 then mn = 0 end
for i in mn..n
if i-(n-i)/(m-1) > w then break end
ret[{"mx"=>i, "mn"=>i, "sum"=>i}] =1
end
return ret
end
# DEBUG
def ptintResults(results)
for r in results
p r
end
end
def solve(m,n,w)
if m == 0 then return 0
elsif m == 1 then return (n>w ? 0 : 1)
end
results = [{{"mx"=>0, "mn"=>0, "sum"=>0} => 1}]
results << init(m,n,w)
for i in 1...(m-1)
results << getNext(results[i], n, w)
end
# ptintResults(results) # DEBUG
return getLast(results.last, n, w)
end
# main
while line = gets
line.strip!
if line.empty? then next end
m,n,w = line.split.map{|a| a.to_i}
p solve(m,n,w)
end
解説
★★★の問題としては標準的な難易度と思います。
ただ、問題がわかりにくいです。
幅0の扱いが問題からはよくわかりません。
実際には切り方が[1,2,3,4,0,0,0]と[1,0,0,2,3,4,0]と[1,0,2,3,4,0,0]は区別されます。
「切れなくなったらやめる」という文言には意味がなく、途中で幅0で切られた場合は区別して考えなければいけないです。
考え方
nを分割して行くのではなく、0〜nまでの任意の数字を積み上げてnにするという風に考えます。
もう一つ重要なのはk人目(1<k<m)まで積み上げた時、その途中のパターンを全て管理する必要はなく、そこまでの合計とケーキのピースのうち最大と最小の値、これらが同じになるパターン数だけを管理すれば良い、ということです。
つまり、3人目まで処理した時に、[1,2,0]と[1,0,2]と[2,1,0](他の0,1,2で作れるパターン全て)は並び順を保持せず、{最大:2, 最小:0, 合計:3}と考えて最大、最小、合計が同じになるパターン数だけを保持するということです。
1人目は0〜nの任意の数を選択します。
2〜(m-1)人目まではそれまでに積み上げられた数の最大から最大-w以内、最小から最小+w以内の任意の数を選びます。そして、選んだ任意の数を加えた最大、最小、合計値を求め、その最大、最小、合計値パターン数を更新します。
m人目はnからそれまでの合計値を引いた値が自動的に選ばれますので、それがそれまでに積み上げた数の最大から最大-w以内、最小から最小+w以内であることを確認します。
最終的に残ったパターン数の合計が答えになります。
solve(m,n,w)
問題の答えを返します。
77〜79は例外パターンの処理です。
m=0の場合は0を返しておきます。
m=1の場合、n>wだとwで切ると必ず余が出るので問題の通りに分割できません。なので0を返します。そうでなければ1パターンしかないので1を返します。
resultsはm回処理した時のパターンを保持する配列です。
81行目で0回目の値を設定していますが86行目のループカウンタを合わせるためのパディングにすぎません。
83行目でinit()を読んで1人目のパターンを生成します。考え方に書いた通り、1人目はwの制約がないので2人目以降とは処理が異なります。
resultsの要素は
{ケーキの最大ピース, 最小ピース, ピースの合計}=>(最大,最小,合計)が同じになるパターン数
です。
85〜87行目のループで2〜(m-1)人目まで、それぞれケーキのピースを積み上げる処理をします。
91行目でm人目のピースがwの範囲内のパターンをカウントし、そのパターン数の合計を返します。
init(m,n,w)
1人目のパターンを作る関数です。
2人目以降の計算量を減らすため1〜nを全て選択するのではなく、範囲を狭めています。
58行目の処理は1人目が選択できるケーキのピースの最小サイズを求めています。1人目が選択できる最小サイズは残りの人が全員(1人目+w)のサイズを選んだ時になります。
61〜64行目のループで1人目が選択できるサイズを列挙していますが、1人目が選べる最大のピースにも上限があります。上限は2人目以降が全員(1人目+1)のサイズを選んだ時になりますので、そのサイズ以上になったらループを抜けます。
列挙したパターンを返します。
getNext(pattern, n, w)
2〜(m-1)人目までが自分のピースを積み上げる処理をします。
引数patternは一人前までに考えられる全パターンです。m,wは入力値です。
変数retは戻り値です。
前回のパターン1つずつに対してループします(6〜21行目)。
変数ptnは{最大、最小、合計}でcntはそのパターン数です。
7行目は選択できるピースの最小サイズを計算しています。ptnの最小-wが選択できる最小サイズですが、0未満にはならないので最小サイズが0未満になったら0にします。
8行目は選択できるピースの最大サイズで、ptnの最大+wになります。
7〜8行目で求めた範囲でピースを選択します(10〜20行目)。
11〜13行目は今回の選択で更新される最大、最小、合計を求めています。mnは最小でptnの最小と今回選択サイズの小さい方、mxは最大でptnの最大と今回選択サイズの大きい方、sumは合計でptnの合計+今回選択サイズになります。
15行目の条件は、
・今回選択したサイズで合計がnを超えない
・今回更新した最大、最小の差がw以下である
場合に、問題の条件を満たすと判断するためのものです。
条件を満たしていれば、戻り値にパターンを追加します。
16行目のnkeyは今回の選択を加えたパターンです。
そして、そのパターンはnkeyがretになければcntに等しく、retにnkeyがあればその値にcntを加えた値になります。retはキーがなければ0を返すので17〜18行目の処理でこの計算を行えます。
今回生成した{最大、最小、合計}ごとのパターン数を返します。
getLast(pattern, n, w)
(m-1)人目のパターンから最後に残ったピースが条件を満たすかをチェックし、条件を満たすパターンの合計を返します。
28行目のretはデバッグのためのもので、m人目が条件を満たした場合にパターンを更新するために使用していますが、問題を解くためには不要です。
countが答えのパターン数合計です。
前回のパターン1つずつに対してループします(31〜50行目)。
34行目で残りのピースのサイズを求めます。
35行目で残りのピースを加えた場合の最小、36行目で最大、37行目で合計(デバッグ用)を計算しています。
最大と最小の差がw以下なら条件を満たしているので(41〜49行目)、答えのパターン数にptnのパターン数をcountに加算します(48行目)。42〜46行目の処理はデバッグ用にm人目のパターンを作っているだけです。
countを返します。これが問題の答えになります。
雑感
結構苦労しました。
最初、nをm個の自然数に分割し、その要素の最大と最小の差がw以下になるパターン数という自然数分割の問題と思いましたが、0の場合でどうも違うんじゃないかと思い直し、問題文の通りに切断して行って途中経過のパターンを(最大、最小、合計ではなく)全て記録して処理するというプログラムを書いたら時間が足りず(かつ間違っている)、という試行錯誤を経てこのプログラムになりました。
こういう風に結果のカウントだけを管理するプログラムはデバッグに必要な情報が消えてゆくので結構辛いものがあります。