CodeIQ:ヘックス上の最長狭義単調増加列
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「ヘックス上の最長狭義単調増加列」(CodeIQ)を参照してください。
問題の概要
【概要】
1辺4マスの六角形状のマス目があり、各マスにはa〜zの文字が入っています。
a〜zの文字は、1〜26 の数を表しています。
適当なマス目から隣のマスへ隣のマスへとたどり、どんどん増えていく数列(狭義単調増加列)を作ることを考えます。
入力で与えられる配置の場合に作ることができる狭義単調増加列の中で、もっとも要素数が多いものの要素数を計算するプログラムを書いてください。
【入出力】
入力は
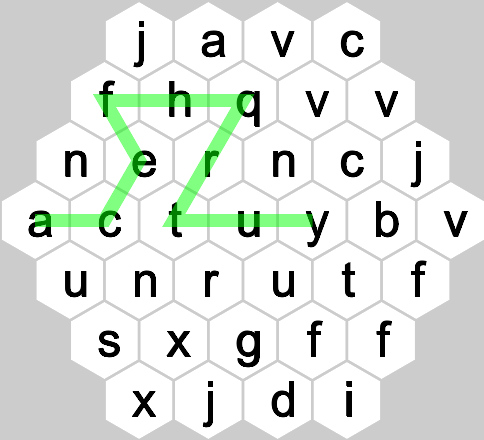
javc/fhqvv/nerncj/actuybv/unrutf/sxgff/xjdiこんな感じで標準入力から来ます。
マス目の東西の一列が、北から順にスラッシュ(/)区切りで並んでいます。
出力は、最長の狭義単調増加列の要素数を、10進数で。
先程の例だと緑色の線が最長となる場合の例になりますので、
10を出力すると正解です。
【例】
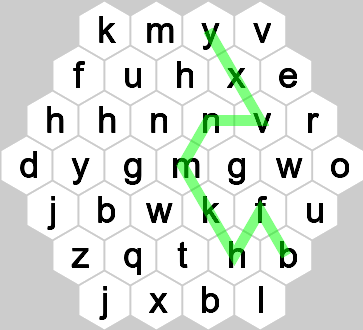
入力 出力 状況 javc/fhqvv/nerncj/actuybv/unrutf/sxgff/xjdi 10 kmyv/fuhxe/hhnnvr/dygmgwo/jbwkfu/zqthb/jxbl 9
【補足】
不正な入力に対処する必要はありません。
長さ1でも狭義単調増加列になります。考えられる最小値は 1 になります。
a, d, f, x のように、ちゃんと毎回増えること。a, n, n, x のようなものは NG。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 入力値からマップを作る
def makeMap(line)
st_pos = [3,2,1,0,1,2,3]
ls = line.split("/")
map = Array.new(7){Array.new(13)}
positions = {}
ls.each_with_index{|l, i|
l.chars.each_with_index{|c, j|
row = i
col = 2*j+st_pos[i]
map[row][col] = c
if positions[c] == nil then
positions[c] = [[row,col]]
else
positions[c] << [row,col]
end
}
}
return [map, positions]
end
# 周囲の値の中で最大のものを返す
def getAroundMax(l, map, results)
ret = 0
directions = [[-1,-1], [-1,+1], [0,-2], [0,+2], [+1,-1], [+1,+1]]
for d in directions
n = [l[0]+d[0], l[1]+d[1]] # 周囲の座標
# 範囲外チェック
if (n[0] < 0) || (n[0] > 6) || (n[1] < 0) || (n[1] > 12) then next end
if map[n[0]][n[1]] == nil then next end
# 次の地点の文字が現在位置以下
if map[n[0]][n[1]] <= map[l[0]][l[1]] then
next
else
v = results[n[0]][n[1]]
if v > ret then ret = v end
end
end
return ret
end
def solve(line)
ret = 0
map, positions = makeMap(line)
result = Array.new(7){Array.new(13,0)}
for a in ('a'..'z').to_a.reverse
if positions[a] == nil then next end
for l in positions[a]
v = getAroundMax(l, map, result)
result[l[0]][l[1]] = v+1
if result[l[0]][l[1]] > ret then ret = result[l[0]][l[1]] end
end
end
return ret
end
# main
while line = gets
line.strip!
if line.empty? then next end
p solve(line)
end
解説
★★★の問題です。
一見、経路探索の問題に見えますが実際は違います。経路探索でも解けると思いますが相当に苦労することになると思います。
考え方
ポイントは2点です。
・ヘクスのマップをどう管理するか
・探索(?)の方法
ヘクスのマップは2次元配列を用意して、1つ飛ばしで使えば良いでしょう。
こんな感じです。
| j | a | v | c | |||||||||
| f | h | q | v | v | ||||||||
| n | e | r | n | c | j | |||||||
| a | c | t | u | y | b | v | ||||||
| u | n | r | u | t | f | |||||||
| s | x | g | f | f | ||||||||
| x | j | d | i |
探索(?)ですが、最初に書いた通り経路探索ではありません。
任意のマスからの経路が定まっている場合、その途中からスタートした場合、途中の地点から最後までは同じ経路にしかならないということです。
例えば例1のaからyまでは10ですが4つ先のhからスタートした場合、そのhからの最長経路は当然6です。このhにはhの右上のaからもajh…と到達でき、このaからの最長経路は8になります。
つまり、任意の地点xからの最長距離nが定まっているなら、その周囲のマスyからxに到達できる場合、yからの最長距離はn+1になります。
そして、マップ上の値はzまでしかないのでzからスタートした場合、結果は1に決まっています。
この2点から次のように処理できることがわかります。
- 全ての地点からスタートした場合の最長経路の初期値を0とする
- z→aの順に地点を選ぶ
- 選んだ地点の周囲を調べ、その中で最大の最長経路+1を地点の最長経路とする
solve(line)
問題の答えを返します。
retは答えの値です。
54行目でマップ(map)とa〜zまでの座標リスト(positions)を作成します。positionsは作らずに毎回マップを舐めて座標を探しても時間的に足りると思いますが一応計算量削減のために作成しました。
53行目は各地点をスタート地点として選んだ場合の最長距離を記録する領域で、マップと同じ大きさの2次元配列になります。
57〜65行目のループでzからaまで降順に最長経路を計算します。
当該文字がなければ無視します(58行目)。
positionsには1文字に対して1以上の座標が記録されているので、その文字の座標の数だけ処理します(59〜63行目)。
getAroundMax()で座標の周囲から最大の最長距離の値を得ます(60行目)。
その値を現在処理中の座標からの最長距離としてresultに記録します(61行目)。
現在処理中の座標の最長距離がretより大きければretを更新します。
答えとしてretを返します。
makeMap(line)
マップとa〜zの座標リストを作成します。
st_posはマップの各行の何番目から値が入っているかを表しています。
lsは入力行を'/'で分割したもの、mapはヘックスマップを2次元配列にした時の領域、positionsは{"a"=>[座標1, 座標2, …], "b"=>[座標1, 座標2, …], …}という文字ごとの座標リストです。
lsの各行について(10〜22行目)、1文字ずつ取り出し(11〜21行目)ます。
文字が書かれるべきmapの行はiですが、列はst_pos[i]が最初の位置で、2文字目からは1つ飛ばしになるのでそれを計算します(12〜13行目)。
mapの座標位置に文字を記録します(15行目)。
positionsに文字ごとの座標リストを追加します(16〜20行目)。
mapとpositionsを返します。
getAroundMax(l, map, results)
引数lの座標の周囲1マスから最大の最長距離を持つ値を調べて返します。
lは[行, 列]の座標、mapはmakeMap()で作成したmap、resultsはsolve()で作成したresultをとります。
変数retは返却値、directionsは周辺の座標を求めるための定数で[左上、右上、左、右、左下、右下]を表します。
全ての方向に対してresultsの値を調べます(32〜46行目)。
周囲の座標を計算します(33行目)。
範囲外をチェックします(36〜37行目)。mapには使っていない領域があるので(各行は1個おきにしか値がない)その領域は無視します(37行目。ただし、ここは通らないはずです)。
周囲の文字がlの座標の文字と同じか若ければ無視します(40〜41行目)。
そうでなければ(42〜45行目)、周辺の座標からresultsの値を取得し、retより大きければretを更新します(43〜44行目)。
retが周辺で最大の最長距離になっているのでその値を返却します。
雑感
問題を見てすぐにキューを使った経路探索でできるなと思って始めましたが、探索ロジックを書き始めてすぐに一度通ったところから先を探索するのは無駄だと気づきました。そのままメモ化するなりしてもできたと思うのですが、ごちゃっとして面倒なので考え直してこのロジックになりました。
単純でわかりやすいロジックになったと思います。