CodeIQ:左と右の有理数
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「左と右の有理数」(CodeIQ)を参照してください。
問題の概要
【概要】
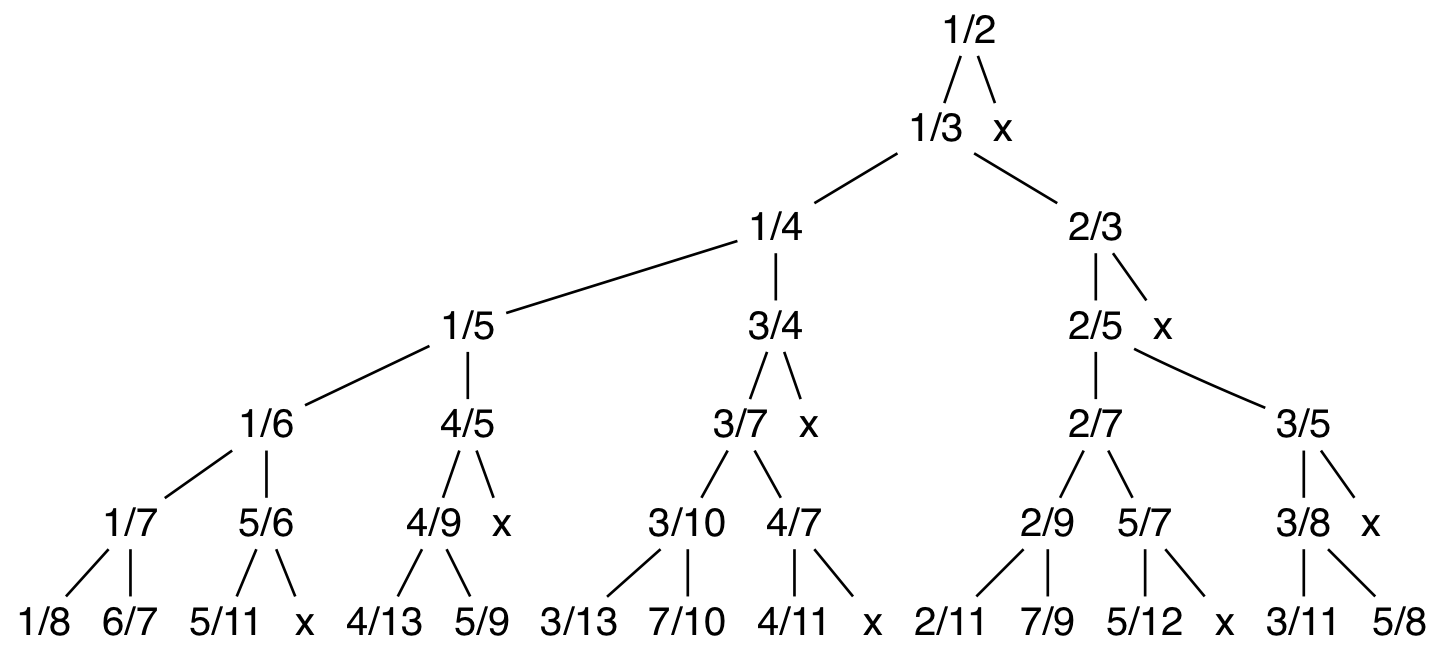
有理数を、図のようにならべます。
図では、紙面の都合で7段目までしか書かれていませんが、下に無限に広がっています。
与えられた有理数の、図上での左隣と右隣(図にある x は無視して)の有理数を求めてください。
【詳細】
有理数を並べるツリーは以下のルールに従っています:
自分が p/q の場合、左の子は p/(p+q)
自分が p/q の場合、右の子は (1-p/q)。ただし、自分が 1/2 以上の場合には右の子はいない。
入力は
3/7
という具合に標準入力から来ます。
出力は、左隣と右隣の有理数を、コンマ区切りで出力してください。
こんな
4/5,2/7
具合です。
ただし、左隣や右隣に有理数がない場合には、そこには有理数の代わりにハイフンをおいてください。
例えばこんな
-,4/5
3/4,-
具合です。
【例】
入力 出力 3/7 4/5,2/7 1/6 -,4/5 2/5 3/4,-
【補足】
不正な入力に対処する必要はありません。
入力の分母・分子 はいずれも正の整数で、分子<分母<二百五十 です。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 親の値を返す
def getParent(v)
if v[0] * 2 < v[1] then return [v[0], v[1]-v[0]]
else return [v[1]-v[0], v[1]]
end
end
# 子供の値を返す
def getChild(v)
ret = []
ret << [v[0], v[0]+v[1]]
if (v[0]*2 < v[1]) then
ret << [v[1]-v[0], v[1]]
end
return ret
end
# 右側の値を探索して返す。見つからない時はnil。
def getRight(v)
depth = 0
nxt = v
root = nil
# ルートになる値を求める
while true
parent = getParent(nxt)
# 1/2までたどったらそれ以上はない
if parent == [1,2] then return nil end
# 右側の子供があるかを確認する
# 右側の子供がなかったらさらに上をたどる
childs = getChild(parent)
if childs.size == 1 then # 親が右側の子を持たない
nxt = parent
depth += 1
elsif childs[1] == nxt # 右側の子が自分自身
nxt = parent
depth += 1
else # 自分が左側の子で右側にも子がある
root = childs[1] # 探索の起点は右側の子
break
end
end
# ルートから左の子をたどる
ret = root
for _ in 0...depth
childs = getChild(ret)
ret = childs[0]
end
return ret
end
# 左側の値を探索して返す。見つからない時はnil。
def getLeft(v)
depth = 0
nxt = v
root = nil
# ルートになる値を求める
while true
parent = getParent(nxt)
# 1/2までたどったらそれ以上はない
if parent == [1,2] then return nil end
# 現在の値が右側になっているかを確認する
# 左側ならさらに上をたどる
childs = getChild(parent)
if childs[0] == nxt then
nxt = parent
depth += 1
else
root = childs[0]
break
end
end
ret = root
for _ in 0...depth
childs = getChild(ret)
# 左右両方の子供がある場合、右側をたどる。一つしかない場合は左側をたどる。
if childs.size == 2 then
ret = childs[1]
else
ret = childs[0]
end
end
return ret
end
# 表示用の文字列に整形する
def getDispStr(v)
if v == nil then return "-"
else return v[0].to_s + "/" + v[1].to_s
end
end
# main
while line = gets
line.strip!
if line.empty? then next end
v = line.split("/").map{|a| a.to_i}
r = getRight(v)
l = getLeft(v)
puts getDispStr(l) + "," + getDispStr(r)
end
解説
★★ではやや難しい方でしょうか。
基本的に2分木の探索なので再帰というのが普通かと思いますが、再帰よりも単純にループで処理した方が簡明です。
考え方
一番簡単な方法はルール通りに計算して表全体を作ってしまうことですが時間が全然たりません。なので、入力から左右の値を求める必要があります。
私の実装は素朴で、右側と左側の値を別々に探索します。
右側の値は次のように探索することができます。
左方向はこの左右反対の処理をします。
- 親の値を計算する。
- 親の値から子の値を計算する。
- 2で計算した子の値の左側と自分が同じなら下方向の探索の起点を右側の子の値にする。
- 2で計算した子の値の右側と自分が同じなら1の値からさらに上を探索する。
- 1/2まで上方向に探索したらやめる(右側の値はない)。
- 下方向の探索の起点が見つかったら、左側の子供を上探索と同じ回数繰り返す。
これで答えを求めることができます。
入力値の制限からツリーの深さは250以下なので上方向、下方向と探索しても500回以下の計算ですから、左右別々に探索しても時間的には大丈夫です。
getParent()
引数vは[分子,分母]の配列です。
この値から親の値を求めるのですが、vが左の子か右の子かわからないと計算できません。
右の値の計算条件に「自分が 1/2 以上の場合には右の子はいない」というのがあるのでこれを利用します。「自分が1/2未満なら右の子がいる」のですが、その値は必ず1/2より大きくなります。そして左の子はp/(p+q)なので1/2以下になります。
なのでvが1/2より大きければ右、そうでなければ左の値として親の値を計算できます。
getChild()
引数vは[分子,分母]の配列です。
返り値は[[左の分子,左の分母], [右の分子,右の分母]]で、右側の値はない場合があります。
計算は問題の通りで、vが1/2以上なら右側の値は計算しません。
getRight()
入力値の右側の値を探索します。
引数vは[分子,分母]の配列です。
depthは探索の深さを管理する変数で、上方向に探索するごとにインクリメントし、下方向に探索するごとにデクリメントします。
nxtは現在フォーカスしている値を保持する変数です。
rootは上方向から下方向の探索に切り替わった時、起点となる値です。例えば入力値が3/4の場合、2/3が最初のrootになります(その親である1/3ではないことに注意してください)。
まず、上方向の探索です。
getParent()で親の値を求め(31行目)、親の値が1/2になるまでループします(30〜49行目)。親の値が1/2になった場合、右側の値は求められないのでnilを返して終わります(34行目)。
その親の値から左右の子の値を求めます(38行目)。
親が子を1つしか持たない場合(39〜41行目)と右側の子の値と現在フォーカスしている値(nxt)が同じなら(42〜44行目)、nxtを親の値に更新し、探索深度を1増やしてループを繰り返します。
それ以外の場合(=親には左右の子の値があって現在フォーカスしている値は左側)ならrootを右の子の値に設定し、ループを抜けます(45〜48行目)。この処理に到達した時点で上方向の探索を終えて、折り返した状態になります。例えば、入力値が3/4なら1/4、1/3とたどってroot=2/3でループを終了します。
rootが決まったら下方向に探索します(52〜56行目)。
こっちは簡単で、rootの値からdepthのカウントと同じだけ左側の子の値をたどれば良いだけです。左側の子の値は必ず存在するので条件分岐などは不要です。
getLeft()
入力値の左側の値を探索します。
引数vは[分子,分母]の配列です。
depthは探索の深さを管理する変数で、上方向に探索するごとにインクリメントし、下方向に探索するごとにデクリメントします。
nxtは現在フォーカスしている値を保持する変数です。
rootは上方向から下方向の探索に切り替わった時、起点となる値です。例えば入力値が3/4の場合、2/3が最初のrootになります(その親である1/3ではないことに注意してください)。
まず、上方向の探索です。
getParent()で親の値を求め(69行目)、親の値が1/2になるまでループします(68〜84行目)。親の値が1/2になった場合、右側の値は求められないのでnilを返して終わります(72行目)。
その親の値から左右の子の値を求めます(76行目)。
現在フォーカスしている値(nxt)が左側の子の値と同じならnxtを親の値に更新し、探索深度を1増やしてループを繰り返します(77〜79行目)。
それ以外の場合(=フォーカスしている値が右側の子の値)ならrootを左の子の値に設定し、ループを抜けます(80〜83行目)。この処理に到達した時点で上方向の探索を終えて、折り返した状態になります。例えば、入力値が3/4なら1/4とたどってroot=1/5でループを終了します。
rootが決まったら下方向に探索します(86〜96行目)。
右側の探索よりは複雑で、子の値が2つある場合は右(91〜92)、1つしかない場合は左(93〜95)の値を辿ります。これをdepthの回数繰り返せば左の値が求まります。
getDispStr()
引数vは[分子,分母]の形かnilなので、nilなら"-"、そうでなければ"分子/分母"の文字列を返します。
main
getRight()とgetLeft()で左右の値を求めgetDispStr()で整形して出力するだけです。
雑感
考え方の方法を見るといかにも再帰的な処理に思えます。
私も最初は再帰で考え始めました。が、これが結構難しいのです。上りの処理と下の処理があるのは再帰呼び出しを上りの処理、リターンで戻ってくる際に下の処理とするのは良いのですが、折り返しの最初(例えば、右側の値を探索する場合、入力値が3/4なら1/4、1/3とたどって2/3になる時)とそれ以降(2/5)を求める時の左右が違うのがややこしいのです。右側の探索の場合、折り返しの時は右側の子でそれ以降は左側としなければいけません。左側の探索時はこの逆です。
この辺で「あー、なんか面倒臭いなぁ。もっと単純にできないかなぁ」と考えていたら、普通にループした方が簡単なことに気づきました。ループで処理すると上りと下りは別のループにしなければならないので、その間で最初の1回だけ違う方向の探索をしてしまえば簡単です。これに気付いた後は特に悩むことなくできました。