CodeIQ:マルチプル・テーブル
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「マルチプル・テーブル」(CodeIQ)を参照してください。
問題の概要
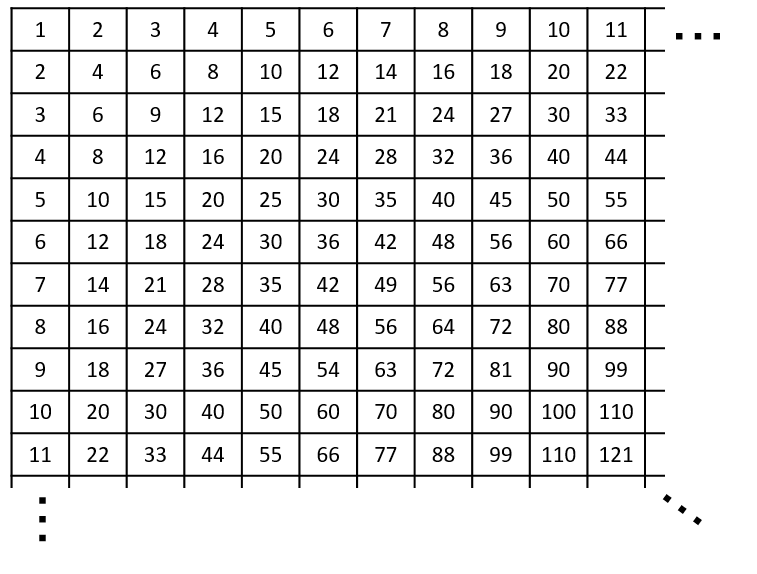
下図のようなかけ算表を考えます。
左上のマスを起点に、右と下にマスがどこまでも続いています。
上から i 行目、左から j 列目のマスには、 i×j の値が書き込まれています。
ここに、罫線に沿った四角形で数字を囲います。
自然数 n に対し、囲われた中の数字の和が n に等しくなるような囲い方の数を F(n) と定義します。
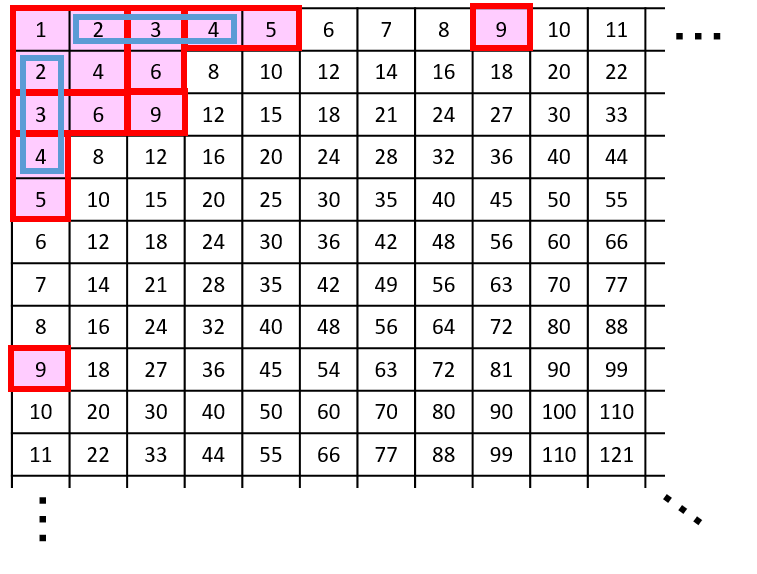
例えば、F(9) = 10 です。題意を満たす囲い方は下記の 10 通りです。
なお、ある囲い方が別の囲い方と部分的に重なっていてもかまいません。
(重なりを見やすくするため、下図では複数の色を使って表しています。)
同様に、F(15) = 16、F(25) = 10 となることが確かめられます。
標準入力から、自然数 n(1 ≦ n ≦ 104)が与えられます。
標準出力に F(n) の値を出力するプログラムを書いてください。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def getDivisor(n)
ret = []
for i in 1..n
if n % i == 0 then ret << i end
end
return ret
end
def countOdds(arr)
ret = 0
for n in arr
if (n != 1) && (n%2 == 1) then ret += 1 end
end
return ret
end
def solve(n)
divs = getDivisor(n)
total = 0
# 1以外の奇数の約数個の連続数に分割できるのでその2倍の数
odds = 2*countOdds(divs)
# printf("1*連続数=%d\n", odds)
total += odds
# 2数の積の形(約数の数に等しい n=x*y=y*xなので約数の数に等しい。n=x^2の場合も問題ない)
total += divs.size
# printf("二数の積=%d\n", divs.size)
# 連続数の積の形になる場合
for x in divs
if (x == 1) || (x == n) then next end
y = n / x
# x*連続数(n!=1)の形になる場合
ox = countOdds(getDivisor(x))
# printf("x*連続数=%d\n", 2*ox)
total += 2*ox
# 連続数*連続数の形になる場合
oy = countOdds(getDivisor(y))
# printf("連続数*連続数=%d\n", ox*oy)
total += ox*oy # 同じ連続数の2乗の形はx*yとy*xで範囲が重複する
end
return total
end
# main
while line = gets
line.strip!
if line.empty? then next end
n = line.to_i
p solve(n)
end
解説
★★★の問題ですが比較的わかりやすいと思います。
とはいえ、プログラミングの前に数学的な知識がないと解けません。
考え方
問題を読んですぐにわかるのが、これは掛け算の表を作ってn*mマス(1≦m,n)で囲める範囲を調べていたのでは絶対に時間が足りないということです。
ならば計算だけで求めるということになりますが、どうすれば良いでしょうか?
まず注目すべき点はnを連続した数に分割する場合、何か法則があるかということです。
例のn=9の場合で考えてみます。
9は2+3+4、4+5、3+6に分けられます。
また、3*3にも分けられます。そして、3は1+2に分けられるので3*(1+2)も当てはまります。
それから(1+2)2=1+2+2+4も当てはまります。
当然、1*9も当てはまります。
つまり、nを連続した数に分割した場合、何パターンに分けられるかがわかれば数を数えられるわけです。そして、これはいかにも調べればわかりそうなので調べました。そうしたら、
「nの約数のうち1以外の奇数の約数の数だけ連続した数の和に分けられる」
ということです。
さて、もう一点だけ確認しておかなければなりません。
約数を連続した数に分割し、その積も連続した範囲に収まりそうですが、n=27の場合(1+2)3のように3つ以上の場合はどうなるかです。これは四角形の範囲に収まりません。なので約数を連続した数に分割したものの積は2つまでを考えれば良さそうです(27の時は3*(1+2)2だけ考えれば良い)。
getDivisor()
nの約数を列挙します。Rubyには素因数分解の関数がありますがn=10000が最大なので単純に全ての数で割ってしまいます。
countOdds()
1以外の奇数の約数の数を数えて返します。
solve()
考え方の通りのプログラムです。
まず、nの約数全てを求めます(21行目)。
次に1*連続した数の和の形になるものを数えます。同様に連続した数*1の形も当てはまるのでnの1以外の奇数の約数数の2倍になります(26行目)。
次に単純に2数の積の形になる場合を数えます。これはnの約数の数に等しくなります(31行目)。例えばn=15の場合、約数は[1,3,5,15]で1*15、3*5、5*3、15*1の4パターンがあり約数の数と同じであることがわかります。
次に連続した数の積になる場合ですが、これはm*(a+b)の形になる場合とl*(a+b)*(c+d)になる場合を考えます。40行目がm*(a+b)の形になる場合で、これは全ての約数に対して、約数を連続した数に分割した場合のパターン数を数えればOKです。45行目がl*(a+b)*(c+d)の場合で選んだ約数とnをその約数で割った値をそれぞれ連続した数に分割した場合のパターン数を掛け合わせればOKです。
あとはこれらのパターン数を合計すれば結果になります。
雑感
全部自力で考えたら非常に難しい(というか、できない)問題だと思いますが、いかにも数学の問題にありそうな「nを連続した数に分割する」という問題だったので調べるのは容易でした。問題は1とn意外に3つの奇数の約数を持つ最小の数が27だったことで、考え方が正しいことを確認するため手でやってみるのが面倒臭かったことです。