CodeIQ:チェックポイントを順番に
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「チェックポイントを順番に」(CodeIQ)を参照してください。
問題の概要
【概要】
東西6マス×南北5マスの地図があります。
マス目には
スタートのマス(s, 必ずひとマスだけある)
ゴールのマス(g, 必ずひとマスだけある)
普通に通れるマス(.)
チェックポイント(1〜9)
通れないマス(X)
があります。
ただし、
移動は、東西南北に隣接しているマスへの移動となります。
一度通ったマスは通れません。
チェックポイントを、1から昇順に全て通ってからゴールしなければなりません。
「X」のマスには入れません。
このルールのもとで、スタートのマスからゴールのマスまで最低何手で到達できるか、その手数を求めて下さい。
【入出力】
入力は
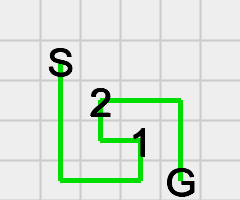
....../.s..../..2.../...1../....g.こんな感じで標準入力から来ます。
マス目の東西の一列が、北から順にスラッシュ(/)区切りで並んでいます。
各文字と意味の対応は下表のとおりです:
文字 意味 s スタート地点 g ゴール . 普通に通れるマス 1〜9 チェックポイント X 通れないマス
出力は、最短の手数を普通に10進数で出力して下さい。
先程の例だと
12という具合です。
ただし、条件を満たしてゴールに到達する方法がない場合には、その旨を示す記号-を出力して下さい。
【例】
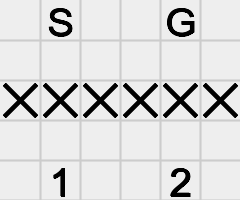
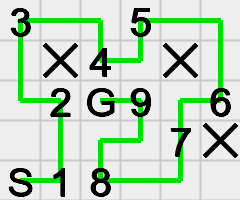
入力 出力 状況 ....../.s..../..2.../...1../....g. 12 .s..g./....../XXXXXX/....../.1..2. - 3..5../.X4.X./.2g9.6/....7X/s18... 24
【補足】
不正な入力に対処する必要はありません。
スタート地点に戻ることはできません。
チェックポイントはかならずひとつ以上あります。
チェックポイントがn個だった場合、1番からn番までが使われます。
途中をとばしたりはしません。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
Map = []
Points = Array.new(9)
$Rows = nil # Mapの行数
$Cols = nil # Mapの列数
$St = nil # スタート座標
$Ed = nil # ゴール座標
class Path
attr_reader :path
def initialize(path=[], pos=[0,0], checks=nil)
@path = path + [pos]
@checks = (checks != nil ? checks.dup : nil)
end
# 位置が到達済みかをチェックする
def checkPos(pos)
return !@path.include?(pos)
end
# posがすでに到達済みの場所ならnilを返す
# posが不正なチェックポイントが不正な場合はnilを返す
# posが未到達ならパスに追加して新しいオブジェクトを生成して返す
def move(pos)
ret = checkPos(pos)
if ret then
nxt = Path.new(@path, pos, @checks)
if nxt.checkPoint() == false then return nil
else return nxt
end
else return nil
end
end
# チェックポイントが順番通りか調べる
def checkPoint()
if @checks.include?(@path.last) then
if @path.last == @checks[0] then
@checks.delete_at(0)
return true
else
return false
end
else
return true
end
end
def clearPoints()
if @checks.size != 0 then return false
else return true
end
end
end
def toMap(line)
ls = line.split("/")
for l in ls
Map << l.split("")
end
$Rows = Map.size
$Cols = Map[0].size
for i in 0...$Rows
for j in 0...$Cols
if Map[i][j] == "s" then
$St = [i,j]
elsif Map[i][j] == "g" then
$Ed = [i,j]
elsif (Map[i][j] =~ /[1-9]/) != nil then
Points[Map[i][j].to_i - 1] = [i, j]
end
end
end
Points.compact!
end
def move(st, ed)
directions = [[-1,0], [1,0], [0,-1], [0,1]]
queue = [Path.new([], st, Points)] # キューには経路情報を保持する
while !queue.empty?
path = queue.shift # これまでの経路情報
cur = path.path.last # 現在の座標
for d in directions
nxt = [cur[0] + d[0], cur[1] + d[1]] # 進んだ場所
# 境界チェック
if nxt[0] < 0 || nxt[1] < 0 || nxt[0] >= $Rows || nxt[1] >= $Cols then next end
# 移動可能な場所かをチェックし、移動可能なら進める
if Map[nxt[0]][nxt[1]] == "X" then next end
npath = path.move(nxt)
if npath == nil then
next
else
if nxt != ed then
queue << npath
else
if npath.clearPoints then
ret = npath.path.size
if ret > 0 then return (ret-1).to_s end # スタートの分を引く
end
end
end
end
end
return "-"
end
# main
while line = gets
line.strip!
if line.empty? then next end
toMap(line)
puts move($St, $Ed)
end
解説
★★の問題ですが難し目と思います。
これまで(2016/8/10現在)に何門か経路探索の問題が出題されていますが、私がやった経路探索の問題の中では1、2を争う難しさだったと思います。
考え方
この問題の難しさは、最適解を求めるためには部分的(チェックポイント間の経路)では遠回りしなければならないことがある、という点にあります。問題の最初の例がちょうど良い例になっており、Sから1まで遠回りしています。
これをいかに解決するか、というのがこの問題の最大のポイントになります。
基本的には幅優先探索です。
そして管理するパラメータは途中地点全ての経路情報になります。
そして次のチェックを行います。
範囲外、Xのマスに入ったらその経路を捨てる。
すでに通った経路を通れないとして判断してその経路を捨てる。
チェックポイント(Gを含む)に到達した時に順番を無視していたらその経路を捨てる。
以上をクリアしてGに最初に到達したものが答えになります。
Pathクラス
経路情報を管理するクラスです。
メンバ変数は次の2つです。
@path:経路情報を座標の配列で持つ。
@checks:未到達のチェックポイントの座標をチェックポイント1から順番に配列で保持する。
Path#initialize()
コンストラクタは引数にそれまでの経路情報(path)、次の地点(pos)、それまでのチェックポイント(checks)をとります。これは移動した時に最大4パターン経路が増えるので、移動するごとに新たな経路情報を作るためです。
Path#checkPos()
引数posの座標[row, col]がすでに通った場所かどうかをチェックします。
単純に@pathに座標が含まれているかどうかを調べ、未到達ならtrue、到達済みならfalseを返します。
Path#move()
引数posの座標[row, col]に移動し、新たなPathインスタンスを返します。移動できない時はnilを返します。
まず、checkPos()ですでに通った場所かどうかを調べます(27行目)。到達済みだったらnilを返し(33行目)、未到達なら次の処理に進みます。
コンストラクタの引数に自身の@path、引数pos、自身の@checksを渡し、@pathにposを追加した経路情報を作成します。
次に、チェックポイントが順番通りかをcheckPoint()で調べます(30行目)。チェックポイントが順番通りでなかったらnilを返し、順番通りなら作成した経路情報を返します。
Path#checkPoint()
チェックポイントを順番通りに通っているかを調べます。
まず、現在の座標がチェックポイントに含まれるかを調べます(39行目)。含まれなければtrueを返します(47行目)。
現在の座標がチェックポイントの場合、@checksの最初の座標が現在の座標と同じかを調べます(40行目)。
同じならチェックポイントを削除し、trueを返します(41〜42行目)。これによって常に@checksの先頭が次に到達すべきチェックポイントの座標になります。
@checksの最初の座標が現在の座標と違う場合はfalseを返します。
Path#clearPoints()
チェックポイントを全て回ったかを確認し、回っている場合はtrue、そうでなければfalseを返します。
@checksの要素(チェックポイントの座標)はチェックポイントに到達するごとにPath#checkPoint()で削除されるので要素が0なら全てのチェックポイントを回ったことになります。
toMap()
入力値を$Mapに保持します。
同時にPointsにチェックポイントの座標を、$Stにスタート地点、$Edにゴールの座標を保持します。$Rowsはマップの行数、$Colsはマップの列数です(固定ですがデバッグ時に小さいマップでテストしたかったので入力値に従うようにしています)。
move()
幅優先探索を行います。
基本的にごく一般的なキューとループを使った方法です。
directionsは進行方向(上下左右)のリストです。
queueは探索候補のPathインスタンスを保持します。初期値はスタート地点1箇所になります。
キューが空になるまでループして探索を行います(86〜114行目)。
queueから経路情報を1つ取り出し(87行目)、現在の座標を取得します(88行目)。
それに対してdiretionsの方向に進めます(90〜113行目)。
進んだ方向の座標を計算します(91行目)。
範囲外なら無視します(94行目)。
Xのマスなら無視します(97行目)。
移動し、移動後の経路を取得します(99行目)。
不正な移動だった(すでに通ったマスに移動した、チェックポイントを飛ばして別のチェックポイントに到達した)場合、npath=nilなのでこの場合は無視します(101〜102行目)。
座標がゴール地点でなければキューの最後に作成した経路情報(npath)を追加します(104〜105行目)。ゴールなら全てのチェックポイントを通ったかをチェックし(107行目)、通っていたら移動回数を返します(107〜110行目)。管理しているのは移動経路でスタート地点からなので-1した値が移動回数になります。
キューが空になって終了した場合はゴールに到達していないので"-"を返します(115行目)。
雑感
最初、問題を斜め読みした時は「なんだ、チェックポイントごとに幅優先探索して結果を足し合わせるだけじゃないか」と思ったのですが、簡単すぎると思って読み直したら「一度通ったマスは通れません」の条件が。これでまず、チェックポイントごとの最短経路だと間違って通れないと判断してしまう場合があるというのに気づき、さらに考えると、部分的には遠回りしなければならない場合がある、というのに気づいて一気に難問になりました。
それで悩んでいる時に、マップが小さいから全パターン試しても時間内に終わらないか? と思ってやってみたときにコードを思いつきました。全パターン試すためには全ての経路情報を保持しなければならないので、そこにチェックポイントの順番チェックを追加し、チェックポイントを順番に通ったもので最初にゴールにたどり着いたのが問題の答えになると気づいたのです。
もし、マップがもっと広くて10×10くらいあったら全パターン試してみようとは思わなかったでしょうからもっと時間がかかったか、諦めていた可能性すらありました。難しかったです。