CodeIQ：まわり将棋に挑戦！

私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「まわり将棋に挑戦！」（CodeIQ）を参照してください。

問題の概要

問題を引用します。

あなたは1人でまわり将棋(Wikipedia)をしています。
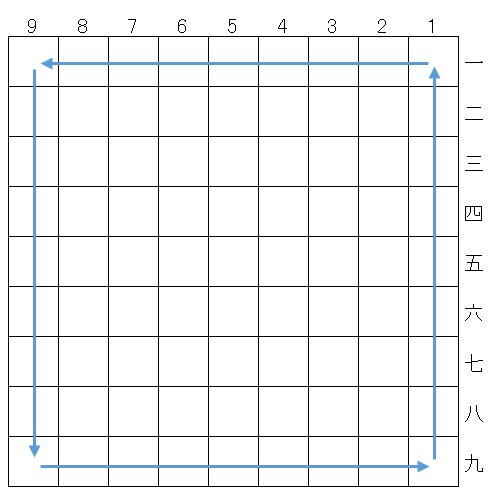
まわり将棋では、あるカド(1一の位置)からスタートして、将棋盤の周囲のマスを移動します。

移動する「マスの数」を決めるために、サイコロの代わりに4枚の「金将」を使います。
将棋盤の上で4枚の「金将」を同時に振り、それぞれの向きで、移動するマスの数が決まります。
「金将」の向きによって、計算の元になる値は以下の通りです。

裏向き：0

表向き：1

横向き：5

上向き：10

下向き：20

（※それぞれの向きについては、Wikipediaを参照してください。）

上記を4枚の金将それぞれについて求め、その「和」が「動くマスの数」になります。
（ただし、裏向きが4枚揃った場合は、8となります。）
例えば、以下のようなマスの数だけ動きます。

金将の向き動くマスの数

表・裏・裏・裏 1

表・表・裏・裏 2

横・表・表・裏 7

横・表・表・表 8

裏・裏・裏・裏 8

上・横・表・裏 16

下・上・横・表 36

なお、振った金将が1枚でも将棋盤から落ちたとき、または金将が重なった場合には無効(0マス)となります。
n 回振ったとき、進める駒がいずれかのカド(1一、1九、9一、9九)にいるようなコマの動きが何通りあるかを求めます。
標準入力から n が与えられたとき、標準出力にその動き方の数を出力してください。

例えば、n=1 のとき、いずれかのカドにいるために動くマスの数は以下の6通りがありますので、6を出力します。
0マス, 8マス, 16マス, 32マス, 40マス, 80マス
（「8」になるような金将の表現は2通りありますが、いずれも同じ位置に動くため1つとカウントします。）

このようにコマの動きに着目するため、例えば n=2 のとき、「1回目に3マス、2回目に5マス」動いたときと、「1回目に5マス、2回目に3マス」動いた場合は別々とカウントします。
※ n は最大で7とします。

【入出力サンプル1】
標準入力

1
標準出力

6

金将の向き	動くマスの数
表・裏・裏・裏	1
表・表・裏・裏	2
横・表・表・裏	7
横・表・表・表	8
裏・裏・裏・裏	8
上・横・表・裏	16
下・上・横・表	36

私のプログラム

Rubyで解答しています。

#!/usr/bin/ruby

def makePattern()
	kin = [0,1,5,10,20]
	memo = [kin]

	for i in 1...4
		memo << []
		memo[i-1].each{|a|
			kin.each{|b| memo[i] << a+b }
			memo[i].uniq!
		}
	end

	return memo[3]
end

def solve(n)
	memo = [{0=>1}]

	for i in 1..n
		memo << Hash.new(0)
		memo[i-1].each{|v, c|
			MovePattern.each{|m|
				memo[i][v+m] += c
			}
		}
	end

	result = memo[n].select{|a| a % 8 == 0}

	return result.reduce(0){|sum, (_, val)| sum + val}
end

#main
MovePattern = makePattern()

while line = gets
	line.strip!
	if line.empty? then next end

	n = line.to_i
	p solve(n)
end

解説

どういう場合に角にコマが存在することになるのかと、計算量を減らす方法がわかればできます。

考え方

まず、角にコマが存在するのは移動量が8の倍数になった場合なのは盤面を数えればすぐにわかります。外周を8マス進むごとに角に到達します。なので、8の倍数になる組み合わせを数えれば良いことになります。

計算量を減らす方法ですが、2段階に分けて減らします。
まず、金将を振った時に進めるマス数は金将の向きによって区別されない（8の場合が2通りあるけれども区別されないことから）ので、進めるマス数のパターンを列挙してしまいます。
そして、n回の移動をした時に何マス目（スタート地点に戻ってもリセットしない）にいるかの履歴を作って動的計画法で解くのですが、この時i回目(1≦i≦n)の位置が同じであればそのカウントだけを管理することで計算量を減らします。

makePattern()

金将を振った時に進めるマス数のパターンを列挙します。
単純に金将が4つあって、1枚につき[0,1,5,10,20]のパターンがあるので全組み合わせを列挙し、重複を削除すれば良いだけです。
全部裏の場合は8と特殊な扱いになっていますが、他にも8の場合があるので0として扱ってしまいます。逆にコマが盤から落ちた場合など進めるマス数が0になる場合をこれでカバーしてしまいます。

solve()

動的計画法で解きます。
引数nは金将を振る最大回数（入力値）です。
memoは添字が金将を振った回数を表し、要素は連想配列でキーがi回目にコマが存在するマスの位置、値がそのマスの位置に到達しているパターン数になります。初期値は0回金将を振った時にスタート地点にいる場合1パターンだけなので{0=>1}を入れておきます。

1〜n回金将を振り（21〜28行目）、1回ごとに前回の位置の全パターン（23行目）に出得る金将を振った時の進めるマス数の全パターンを加えて（24行目）新たな位置を作成します（25行目）。この時、現在の試行回数の結果にそのマス目が存在したらカウントだけを増やします。また、加算されるパターン数は前回のマス目に到達したパターン数になります。

指定された回数まで試行したら結果リストの最後の要素の中で8の倍数のマス目にいるものだけを抽出し、そのカウントを抽出し（30行目）、それを合計して返します（32行目）。

雑感

シンプルな問題だと思います。1回で正解しましたが、何かミスしていてダメだった時は苦労しそうな問題です。金将を振った時に進めるパターン数が多く、それも試行回数によって一気にパターン数が増えるため結果を見てデバッグするのが辛いタイプの問題だと思えるからです。
CodeIQの問題の大半は巨大な組み合わせを求める、多数のパターンから最適解を探す、などの問題が多いためステップ実行でのデバッグはほとんど役に立たないですが、小さいnでもパターン数が多くなるような問題は途中結果をログ出力して追いかけるのも辛いので緊張します。