CodeIQ:100問目!100人限定!百マス計算!
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「100問目!100人限定!百マス計算!」(CodeIQ)を参照してください。
問題の概要
算数の計算練習によく使われる百マス計算。
百マス計算では、図のように縦10×横10のマスがあり、その上と左にそれぞれ0~9の数がランダムに書かれています。
縦と横の交差したマスには、上端と左端にある数の和を書きます。。
このマスをすべて埋めたあと、左上からスタートして右下の数字まで、隣り合うマスを上下左右に辿りながら進みます。
このとき、通過したマスに書かれた数の和が最小になるような経路を求めるプログラムを作成してください。
標準入力の一行目には上端、二行目には左端に書かれる数をそれぞれコンマ区切りで並べます。
通過したマスに書かれた数の和を出力してください。
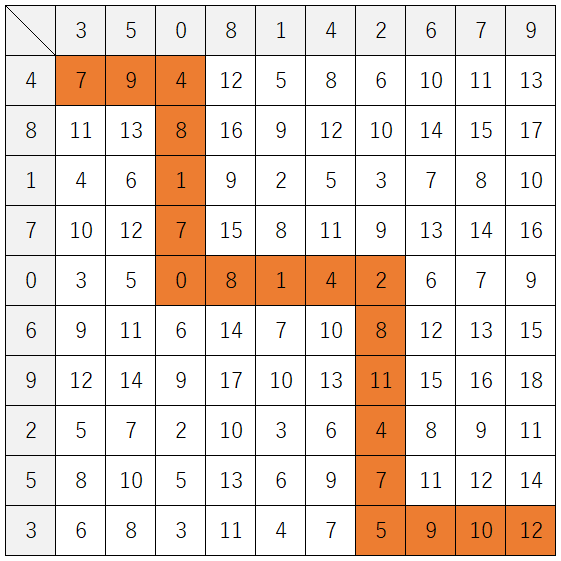
上の図のような場合、下の図のように辿ると最小になりますので、通過したマスに書かれた数の和である117を出力します。
上記の場合、以下のような入出力になります。
【入出力サンプル1】
標準入力
3,5,0,8,1,4,2,6,7,9標準出力
4,8,1,7,0,6,9,2,5,3
117
なお、上と左に書かれる数は1桁(0~9)で、重複する場合もあります。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
# 100マス計算を行う
# @param row 行(縦)の数列
# @param col 列(横)の数列
# @return 計算結果の2次元配列
def makeMap(row, col)
map = []
for r in row
arr = []
for c in col
arr << r + c
end
map << arr
end
return map
end
# 最短距離を求める
# @param map 100マス計算の結果
# @return ゴール時の最小コスト
def solve(map)
memo = Array.new(map.size){ Array.new(map[0].size, 65535) }
directions = [[-1,0], [1,0], [0,-1], [0,1]]
# 最初の位置のコストを設定し、キューに出発地点を入れる
memo[0][0] = map[0][0]
queue = [[0,0]]
# 基本的に幅優先探索
while !queue.empty?
cur = queue.shift
for d in directions
nxt = [cur[0] + d[0], cur[1] + d[1]]
# 範囲外チェック
if nxt[0] < 0 || nxt[1] < 0 || nxt[0] > 9 || nxt[1] > 9 then next end
# 最小コストでメモを更新
val = memo[cur[0]][cur[1]] + map[nxt[0]][nxt[1]]
if val < memo[nxt[0]][nxt[1]] then
memo[nxt[0]][nxt[1]] = val
queue << nxt
end
end
end
return memo[9][9]
end
# main
input = []
while line = gets
line.strip!
if line.empty? then next end
input << line.split(",").map{|i| i.to_i}
end
map = makeMap(input[1], input[0])
p solve(map)
解説
この出題者の問題としては比較的やさしい問題と思います。
また、私がCodeIQの問題をやり始めて始めて出題者による採点(自動採点ではない)の問題でした。
考え方
典型的な最小コスト経路を求める問題です。
100マス計算の結果が各地点を移動するためのコストで、スタート地点が左上、ゴールが右下になるように探索すれば良いわけです。
経路探索はダイクストラ法でOKです。
makeMap()
入力値を実際に100マス計算してマップとします。
特に難しい部分はないと思います。単に行と列の値をたし合わせて行くだけです。
solve()
マップに基づいて問題を解きます。
引数mapはmakeMap()で作ったマップです。
変数memoは任意のマスに到達するための最小コストをメモするための領域です。初期値は非常に大きな値(今回は65535)でmemo[0][0]はmap[0][0]と同値です。初期値を非常に大きな値にしておくのはmemo更新処理を単純にするためです。
directionsは進むべき方向(上下左右)を表す定数です。
queueは探索すべき座標を保持するキューで、初期値は[0,0]になります。
探索はqueueが空になるまでです。queueが空になるのは全ての座標に到達するための最小コストが定まった時になります。
queueから値を取り出して、その上下左右の値をたし合わせます(36〜48行目)。
nxtは上下左右いずれかの座標を示します。範囲外になった場合処理する必要がないので範囲外は無視します(40行目)。
範囲内なら現在の値にnxtの座標の値を加えます。そしてその値が現在のその座標に到達するためにかかったコスト(memoの当該座標の値)より小さければmemoの値を更新します(最初65535で初期化されているので1回目の計算結果では必ず更新されます)。
値が更新された場合はqueueにnxtの座標を追加し、次のループで計算対象になるようにします。
最終的にmemo[9][9]の値が答えになるのでこれを返します。
雑感
出題者が実際にコードを見てコメントをつけてくれる問題ですぐに結果がわからないため、自信はありましたが間違ってないだろうな、と若干の不安もありました。フィードバックをみると出題者の想定通りのアルゴリズムで正解でした。コードがRubyらしくないとのコメントを頂きましたが、読みやすいコードと評価していただいたのは嬉しく思います。私は、もともとがJavaかC/C++のプログラマなので気にしないで書くとそういう感じのコードになってしまいます。なんでJavaやC/C++で書かないかって? コンパイルが面倒くさいもの。
フィードバックによると上と左方向は調べる必要がないとのこと。確かにその通りです。みるからに計算量が余裕だったので問題の通りに実装することしか考えていませんでした。
しかし、フィードバックがかなり丁寧に書かれていて驚きました(後半の模範解答の解説はみんな同じだとは思いますが)。これ、100人分もやるのは大変でしょう。頭が下がります。