CodeIQ:トライアングル・メイズ
私自身が表題の問題を解いた時のプログラムについて解説します。
問題の詳細は「トライアングル・メイズ」(CodeIQ)を参照してください。
問題の概要
次のルールで生成される迷路を考えます。
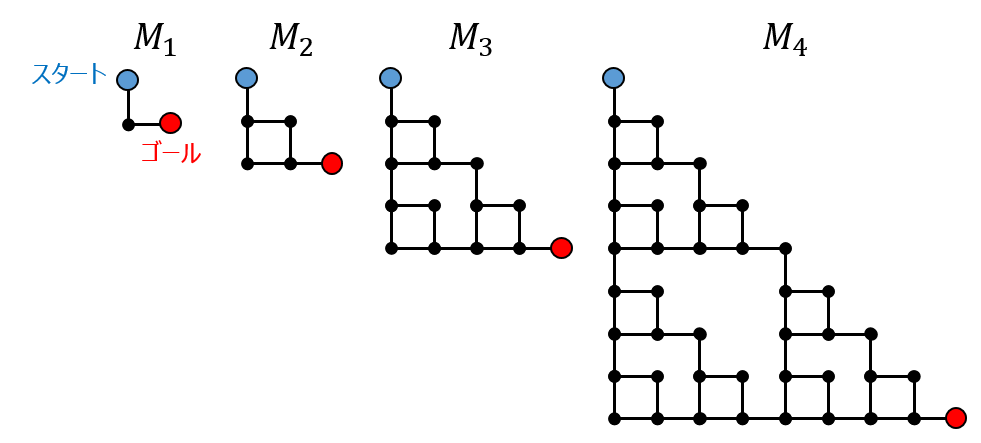
レベル 1 の迷路から始めましょう。レベル 1 の迷路を M1 と呼びます。M1 は、3 つの点を L の字の形につないだものです。
左上の点がスタートで、右下の点がゴールです。
レベル 2 の迷路 M2 は、M1 を 3 つつなげて作ります。
M1 を 1 つ置き、さらにその上と右に 1 つずつ M1 をつなげたものです。
左上の点がスタートで、右下の点がゴールです。
レベル 3 の迷路 M3 は、M2 を 3 つつなげて作ります。
M2 を 1 つ置き、さらにその上と右に 1 つずつ M2 をつなげたものです。
左上の点がスタートで、右下の点がゴールです。
以降同様に、レベル k の迷路 Mk を、レベル k-1 の迷路 Mk-1 を 3 つつなげることで定義します。
さて、この迷路を、点と線をたどってスタートからゴールまで着く方法を考えます。
自然数 n に対し、迷路 Mn を最短距離でゴールするたどり方の数を F(n) と定義します。
例えば F(1) = 1,F(2) = 2 です。
同様に、F(3) = 6,F(4) = 42 です。
さらに、F(10) を 1000003(=106+3) で割った余りは 998593 となることが確かめられます。
標準入力から、自然数 n(1 ≦ n ≦ 108)が与えられます。
標準出力に F(n) を 1000003 で割った余り を出力するプログラムを書いてください。
私のプログラム
Rubyで解答しています。
#!/usr/bin/ruby
def makeAnsList()
ans = [0,1]
memo = {
0 => 0,
1 => 1,
}
for i in 2..100000000
x = (ans[i-1] * (ans[i-1] + 1)) % 1000003
if
memo[x] != nil then break
else
memo[x] = i
ans[i] = x
end
end
return [memo[x], ans.size, ans]
end
def solve(n)
st, ed, memo = makeAnsList()
if n <= ed then return memo[n]
else
cycle = ed-st
pos = ((n-st) % cycle) + st
return memo[pos]
end
end
# main
while line = gets
line.strip!
if line.empty? then next end
p solve(line.to_i)
end
解説
★★★の問題だけあって相応に難しいです。
この問題の難しさは3点あります。
- そもそも経路のパターン数を求めるのに数学的能力を要求される。
- 経路のパターン数の値があっという間に大きくなる(Rubyだとn=20の段階でCtrl+Cでプログラムを止めるくらい時間がかかってしまう)。
- 最大108は単にループをカウントするだけで(C言語でやったとしても)時間的に間に合うかどうかというレベル
考え方
まず、経路のパターン数を求められなければ話になりません。
OEISで調べたくなりますが、OEISで調べるために実際に探索して経路のパターン数を求めるプログラムを作ること自体が結構な難問です。仕方ないので数学の問題として考えました。
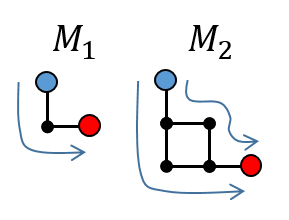
上と右に「L」の経路を追加して3つの経路をつなげるのですが、F(n)のマップに含まれるF(n-1)の経路を上、左、右と呼ぶことにします。下図のような感じになります。
(左)┗┗(右)
左の経路を考えずに上の経路と右の経路だけを間変えた場合の経路のパターン数をF'(n)とすると、
F'(2) = F(1)*F(1)
です。
同様にF'(3) = F(2)*F(2)です。
ということは、
F'(n)=F(n-1)*F(n-1)
になりそうです。
この考え方は正解です。なぜなら、F(n)のマップのF(n-1)で構成される上の部分のゴールは右の部分のスタートに繋がっていて、必ずこの地点を通らないと上の部分から右の部分に行くことができません。なのでF'(n)=F(n-1)*F(n-1)になるのです。
次に左部分を通る場合を考えます。
これをF''(n)とすると、
F''(n) = F(n-1)
になります。
なぜなら、F(n)のスタート地点から左部分のF(n-1)のマップのスタート地点にたどり着く方法はまっすぐ下に向かった場合1通りしかありません。そして、左部分のF(n-1)のマップのゴール地点からF(n)のゴール地点にたどり着く方法はまっすぐ右に進む1通りしかありません。なのでF''(n) = 1*F(n-1)*1 = F(n-1)となります。
F(n) = F'(n) + F''(n)なので、
F(n) = F(n-1)*F(n-1) + F(n-1)
となります。
さて、この式を使って求められる値は2nのオーダで大きくなります。
Rubyだと任意精度整数が自動的に利用されるので桁溢れは問題ないにしても、計算速度が全然たりません。問題は1000003で割った余りを求めよ、なので余りだけを計算するようにしなければなりません。
ここで、ある数aをxで割った場合を考えます。
a=bx+c (b,cは正の整数)
と表すことができます。
F(n) = bx+cだったとすると、F(n+1) = (bx+c)2+(bx+c)です。
これを展開してxでまとめます。
F(n+1) = (bx+c)2+(bx+c)
= b2x2+2bcx+c2+bx+c
= x(b2+2bc+b)+(c2+c)
よって、F(n+1)/xの剰余は
(c2+c)/xの余り
になります。
つまり、F(n)/xの余りだけを使ってF(n) = F(n-1)*F(n-1) + F(n-1)と同じ計算を適用すると余りだけを求めることができます。
さて、最後の問題、108回の計算量をいかにして減らすかです。
F(n)/1000003の余りのパターン数は1000003よりも少ないことは明らかです(余りとして取り得る数値は1〜1000002しかありません)。ということは、余りの数を列挙した場合、どこかで同じ数が現れます。そして、先に説明したF(n)/1000003を求める計算式はF(n-1)/1000003の結果だけから求められるので、同じ数が余りに登場したら、そのあとは同じパターンの繰り返しになる、ということを意味します。
なので、初めて同じ数が余りに現れるまで計算しておいて、あとはその結果から繰り返した先の値を検索して返せば良いということになります。
以上のロジックで答えを求められるので、あとはこれをプログラムにするだけです。
makeAnsList()
繰り返しが現れるまでのF(n)/1000003の数列を作ります。
返り値は[繰り返しの先頭番号, 数列のサイズ, 余りの数列]です。
ansは余りの数列でn=0,1の時の値を初期値としています。
memoは余りの値が再登場したかをチェックするための連想配列で{余りの値=>ansの添字}となっています。
最大108ループし(10〜19行目)、F(n)/1000003を計算します(11行目)。
計算式は「考え方」に書いた通りです。
そしてmemoに余りの値があったらループをやめます(13〜14行目)。なければmemoに値とansの添字を記録し、ansに余りの値を追加してループを継続します(15〜18行目)。
solve()
makeAnsList()で答えの値リスト(memo)、繰り返しのスタート番号(st)、リストのサイズ(ed)を取得します(25行目)。
nがed以下(=繰り返しになる前)ならmemoの当該位置の値を返すだけです(27行目)。
nがedより大きければmemoのどの値が答えか、位置を計算して求めます(28〜32行目)。
まず、繰り返し周期(cycle)はed-stになります(29行目)。
0〜stまでの値は繰り返されないので(n-st)が繰り返される範囲になります。そして、周期がcycleなので(n-st)%cycleが繰り返しの開始点から何番目かを表します。memoの0〜stまでは繰り返されない値なのでそれを加えて、((n-st) % cycle) + stが求める位置になります(30行目)。
あとは求めたmemoから位置の値を返せばOKです。
雑感
難しかったですがスッキリ解けて満足です。
ちなみに、このプログラムの前に余りだけを計算する(余りの繰り返しを表引きにしないで108まで余りだけを計算する)プログラムをC言語で書いて投稿して時間切れになっています。
C言語で書いた最後まで計算するコードはローカルで1.3秒余りだったのですが、CodeIQの実行環境が新しくなって以降ローカルより少し早いのでひょっとしたら? と思って投稿してみました。結果はテストケースの最悪のパターン(n=108)でダメでした。
C言語でダメなら他の言語でも同じアルゴリズムはダメなので(Fortranなら可能性はあると思いますが言語の選択対象からなくなってしまった)、もう少し考えてこのコードになりました。
実際のところ、繰り返しになるというのはC言語で書く前には想定していたのですが面倒臭かったので手を抜いてみたらやはりダメだったということです。まぁ、C言語のコードが通っていてもスッキリはしないのでこれでよかったと思います。